Natural Frequency Calculator
(DnV guidelines 14)
This calculator provides the same information as Mode Shapes but according to DnV guidelines 14.
Pipelines laid over an uneven surface will inevitably lead to sections (lengths) that span gaps in the supporting terrain causing them to sag locally (Fig 1) and affecting their natural frequency; an attribute applicable to every elastic structure.

The mode shape of any structure vibrating at (or close to) its natural frequency will be amplified according to a natural relationship as shown in Fig 2 dependent upon its damping ratio (ξ).
The difference between Mode 14 and Mode Shapes is that this calculator includes the effect of axial force but only estimates the other properties of the vibrating pipeline. Mode Shapes, however, does not include the effects of axial force but accurately calculates all the other properties of the spanning element.
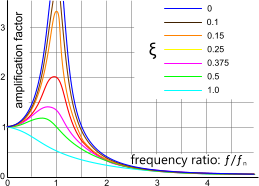
Fig 2. Effect of Damping on Mode Shape
DnV suggests the accuracy of their formula to be ±30% of the expected natural frequency but only if the two qualifying requirements are met: i.e.
L/D < 200 and C₂.Sᵉᶠᶠ/Pᴱ > -0.5
It should be noted, however, that such accuracy is very much dependent upon the interpretation of DnV's end condition Coefficients; C₁, C₂ & C₃ that apply in combination. DnV's calculation assumes an applied (active) axial force but ignores any resultant growth/shrinkage.
End Condition Coefficients
DnV applies coefficients in their natural frequency formula to account for bending, axial and sagging stiffnesses, each of which needs to be selected carefully for best results.
C₁ (bending)
This coefficient is a factor that should be applied to incorporate the effect end conditions will have on the bending stiffness of a spanning pipeline.
If both ends of the spanning pipeline are allowed to freely rotate (pinned) about their supports (highly unlikely), DnV recommends the use of 1.57 for this coefficient. If, on the other hand, both ends are totally fixed and absolutely no rotation is possible (also unlikely), DnV recommends the use of 3.56
In reality, the most appropriate value will be somewhere in between. If no suitable information regarding the end conditions is available, DnV recommends C₁ = 2
C₂ (axial force)
This coefficient is a factor that should be applied to incorporate the effect end conditions will have on the axial force (ᵉᶠᶠ) or axial stiffness of a spanning pipeline.
If both ends of the spanning pipeline are allowed to freely rotate (pinned) about their supports (highly unlikely), DnV recommends the use of 1 for this coefficient. If, on the other hand, both ends are totally fixed and absolutely no rotation is possible (also unlikely), DnV recommends the use of 0.25
In reality, the most appropriate value will be somewhere in between. If no suitable information regarding the end conditions is available, DnV recommends C₂ = 0.5
C₃ (sag)
This coefficient is a factor that should be applied to incorporate the effect end conditions will have on the sag in a spanning pipeline.
If both ends of the spanning pipeline are allowed to freely rotate (pinned) about their supports (highly unlikely), DnV recommends the use of 5.0E-03 for this coefficient in a non-operational pipeline or 5.0E-04 if operational. If, on the other hand, both ends are totally fixed and absolutely no rotation is possible (also unlikely), DnV recommends the use 5.0E-05 of for this coefficient in a non-operational pipeline or 5.0E-06 if operational.
In reality, the most appropriate value will be somewhere in between. If no suitable information regarding the end conditions is available, DnV recommends C₃ = 1.0E-04 for this coefficient in a non-operational pipeline or 5.0E-05 if operational
Sᵉᶠᶠ (effective axial force)
The axial force in a pipeline is due to a combination of internal and external pressures, body temperature and residual lay-tension together with any independently applied axial force. DnV recommends the following calculation options:
Sᵉᶠᶠ = Nᵗʳ - pᵢ.Aᵢ + pₑ.Aₑ for a partially restrained pipeline (i.e. normal conditions)
Sᵉᶠᶠ = Hᵉᶠᶠ - Δpᵢ.Aᵢ.(1-2.ν) - Aˢ.E.ΔṮ.αₑ for a pipeline totally restrained, i.e. the ends of the spanning pipe cannot move in any way whatsoever.
Sᵉᶠᶠ = 0 for a pipeline totally unrestrained, i.e. the ends of the spanning pipe can grow and shrink without constraint of any kind.
CalQlata has interpreted the above as follows:
Sᵉᶠᶠ = Nᵗʳ - pᵢ.Aᵢ + pₑ.Aₑ - Aˢ.E.ΔṮ.αₑ in which Nᵗʳ should be entered as a negative value for a compressive force and a positive value for a tensile force.
If Nᵗʳ, pᵢ, pₑ & ΔṮ are all given a value of zero, Sᵉᶠᶠ will also equal zero.
Q (deflection load)
DnV provides for the application of a deflection load (per unit length) either due to a flowing current (Qᶜ) or the pipe's submerged weight (Qʷ).
You will normally see little difference in the calculated natural frequency (ƒ₀) of a pipline for either deflection loading condition.
Qᶜ (current)
Water (or any fluid) flowing across a pipe will cause it to deflect due to drag. If there is no significant acceleration present in the moving current, the added mass component may be ignored. The current deflection load (per unit length) is calculated as follows:
Qᶜ = ½.Cᴰ.ρᵐ.D.v² (+ ¼.Cᴹ.ρᵐ.Aₑ.a = 0)
(drag coefficient, medium density, pipe coating outside diameter, fluid velocity)
Qʷ (weight)
The weight of the pipeline means its buoyant mass multiplied by gravitational acceleration. The weight deflection load (per unit length) is calculated as follows:
Qʷ = g.(mᵖ + mᶜ + mᶠ + mᵃ)
(acceleration due to gravity, pipe mass, coating mass, fluid mass and displaced mass of surrounding medium {medium density multiplied by total pipe cross-sectional area})
Mode 14 Calculator - Technical Help
Units
You may use any units you like, but you must be consistent.
However, accelerations must be entered 'per second'.
Input Data
Nᵗʳ = residual (post-lay) axial tensile⁺ᵛᵉ/compressive⁻ᵛᵉ force in the pipeline including any additionally induced axial force
Dˢ = outside diameter of the pipeline excluding coating
tʷ = wall thickness of the pipeline
tᶜ = wall thickness of the external coating
L = length between touch-points of the pipeline along the unsupported span
pᵢ = pressure of the internal fluid
pₑ = pressure of the external fluid in which the pipe is immersed
δṮ = temperature difference, between post-lay and operational conditions
v = external fluid velocity [per second]
C₁ = DnV coefficient for bending stiffness (1.57 < C₁ < 3.56)
C₂ = DnV coefficient for axial stiffness (1 < C₂ < 0.25)
C₃ = DnV coefficient for sag (as laid: 5E-03 < C₃ < 5E-05; operational: 5E-04 < C₃ < 5E-06)
E = Young's modulus of the pipeline material
αˢ = coefficient of linear expansion of the pipeline material
ρˢ = density of the pipeline material
ρᵐ = density of the surrounding medium
ρᶠ = density of the internal fluid
ρᶜ = density of the pipeline coating
g = gravitational acceleration [per second squared]
Output Data:
ƒ₀ = natural frequency of the submerged free spanning pipeline
qual₁ = DnV qualification value; C₂.Sᵉᶠᶠ/Pᴱ {>-0.5}
qual₂ = DnV qualification value; L/D {<200}
I = second moment of area of pipeline excluding coating
D = outside diameter of pipeline including external coating
Aᵢ = cross-sectional area of pipeline bore
Aₑ = cross-sectional area of outside diameter of pipeline including external coating
mₑ = effective mass of pipeline (including added mass)
Lᵉᶠᶠ = effective length of free span in pipeline {1.0 x L < Lᵉᶠᶠ < 1.12 x L}
Sᵉᶠᶠ = effective axial force in pipeline
Pᴱ = Euler buckling load of free span length
Qᶜ = horizontal lateral force in pipe due to v
Qʷ = vertical lateral force in pipe due to mₑ
Applicability
Mode 14 applies to the free spanning length of any submerged pipeline that complies the qualification requirements (qual₁ and qual₂)
Accuracy
Accuracy of this calculator is expected to be ±30% of the true value if the free span complies with DnV qualification requirements (qual₁ and qual₂)
Further Reading
You will find further reading on this subject in reference publications(67)

