Added Mass & Drag Calculator (incl. inertia)
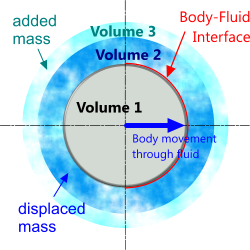
Fig 1. Inertia Coefficient (Ci)
Movement of a body through a fluid (Fig 1) will be resisted by;
a) Drag: friction at the 'Body-Fluid' interface
together with
b) Inertia: the mass of fluid displaced by the body
This resistance is the force induced on a submerged body (see CalQlata's Fluid Forces) and is defined by its shape and surface quality.
Added Drag determines the Drag and Inertia shape coefficients that may be used to calculate such forces.
Drag Coefficient (Cd)
Drag on the body comes from the interface between its surface and the resistance to shear of the fluid in which it is immersed. There are four fundamental influences in the amount of drag experienced:
1) Resistance to shear in the fluid: Which can be established using the Reynolds number (see CalQlata's Fluid Numbers calculator) if your operational conditions fall within the parameters of relevant experimental work. For example, you will find many references to the graph provided in Fig 2, which is valid for Reynolds numbers up to 1E6 and from which a linear relationship can be derived up to 100. However, as most practical applications produce Reynolds numbers considerably higher than this, its use for solving practical engineering problems is limited.
Shear resistance in a liquid and friction between a liquid and a solid is actually due to inter-atomic magnetic forces.
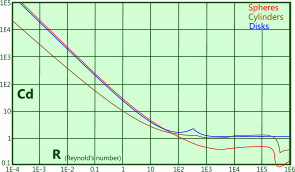
Fig 2. Drag and Reynolds Number Relationship
2) Surface roughness: A smooth surface has a much smaller surface area than a rough surface, therefore, resistance to fluid shear (see 1) above) will also be considerably less.
For clean machined, forged or painted surfaces in relatively good condition, there is no need to apply an additional coefficient of friction to 'Cd'.
For badly pitted and/or corroded surfaces or very fast/turbulent flow conditions, it is usual to apply an additional factor thus;
Cd' = Cd.(1+ƒ)
where; Cd' is the modified drag coefficient and ƒ is Colebrook's friction factor
3) Shape: If a perfectly smooth body is passed through a fluid with no resistance to shear, the shape of the body would have no influence on drag, which would be zero under such circumstances. However, as all fluids have resistance to shear and there is no such thing as a frictionless surface, forces on a body from relative movement in a fluid will always be influenced by both shape and surface condition.
4) Free-Flow: If a body is placed close to a structure sufficiently large and solid to prevent fluid flowing freely around all sides, such as a seabed or wall (Fig 3), fluid shear resistance will increase. It is expected that where gaps (Fig 3 'h') are less than the principal sectional dimension of a body (e.g. Fig 3 'd') the resistance will increase up to a maximum when the two surfaces make contact and the flow around one side of the body is totally prevented. Separation ('h') greater than 'd' will have minimal effect on drag.
Numerous shape coefficients are used in Added Drag for the force calculations of common structural sections (circular, rectangular, etc.) accounting for the effects of drag (Cd), and suitable factors are applied to these coefficients to include the effects of normal surface condition and obstruction proximity.
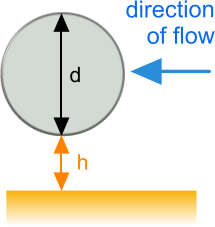
Fig 3. Close Boundary Effect
Inertia Coefficient (virtual mass) (Ci)
Virtual mass describes the total expected mass of disrupted fluid as an immersed body travels through it. This total value comprises two parts (Fig 1; Volume 2 + Volume 3):
Note: Volume (described above) should be interpreted as volume per unit length
1) Actual displaced mass: This is a volume of fluid exactly equal to the volume of the body displacing it (Fig 1; Volume 2) and its coefficient is equal to 1.0, which Ci would also equal if the body was stationary.
2) Added Mass (Ca): As soon as the body moves, however, there will be an additional mass of fluid (Fig 1; Volume 3) disrupted by the actual displaced mass (Fig 1; Volume 2). Again, the amount of disruption will be dependent to some extent on the viscosity of the fluid (and hence its Reynolds number).
To summarise: Ci = 1+Ca
Like Drag, Added Mass is also influenced by shape (see Drag 3) above) and proximity (see Drag 4) above) and can be accommodated with suitable factors.
Added Mass & Drag Calculator - Technical Help
Surface Condition
Surface roughness (ϵ), i.e. the depth of surface irregularities, is applied in Added Drag as a ratio of surface roughness to a representative sectional dimension 'D' {where D=(a+b)/2}.
Where the surface finish is of considerably poorer quality than cast, machined, forged, etc. (i.e. flame-cut, concrete, corroded, etc.) and/or the fluid is fast flowing, an additional factor should be applied, see Drag, 2) above.
The above mentioned factors that account for: surface condition (Drag only), shape and proximity are automatically included in Added Drag calculations.
Applicability
The factors provided in this program relate to applications in normal homogenious fluids such as air or water. They may not be suitable for fluids with significantly different properties such as those containing solids or with bonding characteristics.
There is now an alternative calculation procedure to that used here (Morison); The State of Matter
Further Reading
You will find further reading on this subject in reference publications(6 & 12)

