RAO Calculator
(vessel response amplitudes)
Response Amplitude Operator
The term Response Amplitude Operator comprises two parts: Response Amplitude and Operator, each of which may be described as follows:

Fig 1. 6-Degrees of Freedom
Response Amplitude; refers to the degree of movement induced in a floating vessel due to a passing hydrodynamic wave and this movement is absolute (or actual)
Operator; refers to a factor that must be multiplied by a specific value; e.g. wave height (or amplitude) in order to define the absolute (or actual) movement
The problem with the Operator is that the Response Amplitude must have a linear relationship with the wave height in order to be accurate, which would only apply if added mass and damping are not included in the calculation
For maximum accuracy, the RAO calculator provides an actual Response Amplitude (RA) at a given angle, time or distance through a wave, not a Response Amplitude Operator (RAO).
The Wave
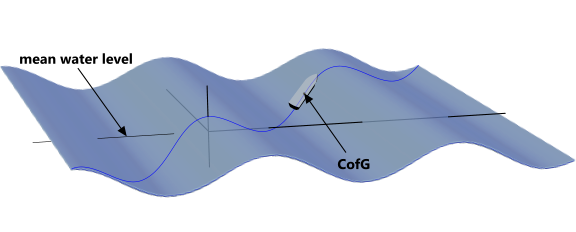
The wave height, water, depth and period all affect the vessel's responses. The amplitude (or wave height) at angle 'θ' through the wave is its surface profile 'η'; i.e.; the height of the surface of the water above mean water level (Fig 2).
RAO calculations are based upon the harmonic excitation of a floating vessel by a passing wave. It is assumed that (after settling down) the vessel will return to the same state at the same angle (θ) through each following [identical] wave.
The Vessel
The vessel can be anything from a floating box to a ship or rowing boat, all of which are subject to the same laws. Its submerged shape will define its response to a wave and its operating mass will always be equal to the mass of water it displaces.
Heading (μ)
A vessel can travel with the wave; μ=0° (a following wave), or it can travel against the wave; μ=180° (a head wave). If μ=0° the wave encounter period will be much longer than if μ=180°, increasing the effective wave length and reducing vessel responses. If μ=90° the vessel is travelling along (parallel to) the wave (Fig 2).
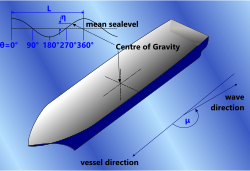
Fig 2. Vessel Heading
Usually but not always, in the event of zero phase lag (see Phase Lags below) maximum displacements will occur at maximum wave elevation or minimum slope, i.e.:
Maximum and minimum Heave would occur at wave peak (θ=0° & 360°) and trough (θ=180°) respectively
Maximum Pitch (μ=0°) or Roll (μ=90°) would occur at maximum wave slope (θ=90° & 270°)
Dimensions
It is normal practice to take vessel length and width (beam) at the water-line.
All vertical dimensions are normally taken from the vessel's keel (lowest longitudinal). The vessel's draft is therefore the height from the keel to the water-line.
It is assumed that the vessel's centre of gravity and centre of buoyancy are always in the same vertical plane/line, both longitudinally and laterally. This is a reasonable assumption because:
a) The vessel would otherwise sit 'tilted' on a flat sea
b) The vessel's ballast can and should be redistributed to achieve verticality
The points of interest on this axis (z) are (Fig 3):
c) The vessel's centre of gravity (CofG)
d) The vessel's centre of buoyancy (CofB)
e) The vessel's metacentric height (GM)
The vessel's CofB may be above or below the CofG but if its GM is negative, the vessel will be unstable. The greater the 'GM', the more stable the vessel. As the beam of a ship is usually less than its length, the lateral GM will usually be less than the longitudinal GM, i.e. the vessel will be less stable laterally than longitudinally, hence it usually rolls more for a given wave amplitude than it pitches.
Centre of Buoyancy
A vessel's centre of buoyancy is the centre of the mass of water it displaces. For example;
The centre of buoyancy of a vessel with a rectangular longitudinal cross-section with be half-way up its draft.
The centre of buoyancy of a vessel with a triangular longitudinal cross-section with be two-thirds of the way up its draft.
It is determined longitudinally by identifying the centre of area every foot or metre from stern to bow, and the moments normalised to find its longitudinal position. Latitudinally it can be assumed to occur at the vessel's centreline.
This position will shift as the vessel rolls and pitches and thereby define the point at which the metacentric height (GM) is established (Fig 3).
The RAO calculator requires a buoyancy height factor (Fᴮ) in order that you can define the vessels CofB. Unless the hull is an inverted triangle, this factor should normally be between 0.5 (rectangular box) and 0.67 (triangular hull) dependent upon its shape.
Centre of Gravity
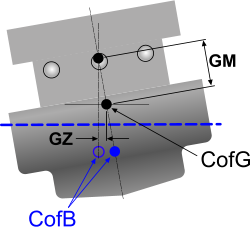
Fig 3. Vessel CofG & CofB
A vessel's centre of gravity is calculated from its mass moments about its three axes; x,y,z
However, this can be shifted slightly by redistributing ballast (e.g. water in its sea chests) until it appears above its centre of buoyancy, thereby eliminating any static tilt (normalising its Trim).
Metacentric Height
The metacentric height (GM) may be considered as a mast of negative weight. The higher it is the more righting assistance the vessel will gain as it tilts. The righting moment is generated by the vessel's buoyancy multiplied by its righting arm (GZ)
Tilt
When travelling in direction μ=0° the vessel will [theoretically] experience zero Roll.
When travelling in direction μ=90° the vessel will [theoretically] experience zero Pitch.
At any other heading, the vessel will tilt at an angle that is a combination of Pitch and Roll, and because Roll and Pitch are at right angles to each other, you can use Pythagoras' theorem to find the maximum [combined] tilt: Tilt = √(Roll² + Pitch²) ...
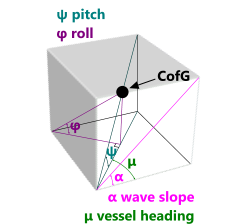
Fig 5. Combined Roll & Pitch
... as long as this calculation is carried out at the same angle through the wave (θ) taking both phase lags (Rᴾᴴ, Pᴾᴴ) into account; i.e. they must occur simultaneously for this calculation to be correct.
For example; you calculate the largest angular response (e.g. Roll) at θ, subtract the phase angle for Pitch from θ and recalculate using this modified θ. The former Roll and the latter Pitch will occur together.
Roll and pitch angles on the surface of a wave can be calculated from the wave profile slope and vessel heading as follows (Fig 5):
ψ = Atan(Tan(α).Cos(μ))
φ = Atan(Tan(α).Sin(μ))
Maximum Tilt: Unless you have a very strange vessel, e.g. wider than it is long, the greatest tilt will occur in Roll (not Pitch) for any given wave.
Therefore, if you need to find the largest tilt for a given vessel in a specified wave you should set the vessel heading (μ) to 90° and the angle through the wave at (θ) to 90° or 270°
In reality the tilt shown in RAO would not necessarily occur at θ=90° (or 270°) it would occur at 90° or 270° plus the phase lag (Rᴾᴴ)
Added Mass
As a vessel moves it pushes water out of the way and sucks water in from behind. This water is the 'added' (additional to the vessel) mass. You will see it referred to in various publications as A11, A22, A33, A44, A55 & A66, which represent the added mass component for Surge, Sway, Heave, Roll, Pitch and Yaw respectively.
A11, A22 & A66 are not included in the RAO calculator as the acceleration of water behind and in front of the moving vessel are virtually equal and opposite (i.e. they cancel each other out).
A33 is the most important and influential added mass component and is calculated in RAO. However, you may prefer to apply your own added mass component as A33 is a compromise based upon the assumption that it is equal in both directions (i.e. upwards and downwards), which is not the case. We have therefore provided the option to enter a value for Ca (A33) which (if entered) will override the calculation (see RAO - Technical Help below).
Damping
As the vessel moves through the water it is dragged back by the contact between the water and the vessel's surfaces. Along with the stiffness of the vessel (see Spring Coefficient below), this 'dragging' will dampen the movement inducing a response lag. You will see it referred to in various publications as B11, B22, B33, B44, B55 & B66, which represent the damping coefficient component for Surge, Sway, Heave, Roll, Pitch and Yaw respectively.
The Damping Ratio (ξ), i.e. the ratio between the damping coefficient and critical damping (normally '0<ξ<1'; values greater than 1 mean over-damped and can work against you), defines the effectiveness of the damping coefficient. The smaller the damping ratio the less its effect.
B33, B44, B55 are calculated in the RAO calculator but you are required to enter lateral and longitudinal drag coefficients (Cd) for B11 (Longitudinal), B22 & B66 (both Tangential) responses (see RAO Calculator - Technical Help below).
Spring Coefficient
A vessel will respond to movement like a spring due to gravitational acceleration that is trying to restore it to its upright condition. You will see it referred to in various publications as C11, C22, C33, C44, C55 & C66, which represent the spring coefficient component for Surge, Sway, Heave, Roll, Pitch and Yaw respectively.
C11, C22 & C66 are not included in the RAO calculator as they are not influenced by gravitational acceleration.
The nature of spring coefficients mean that a vessel will have a natural frequency (ƒⁿ) that, dependent upon the damping ratio (ξ), could cause it to oscillate out of control thereby making it unstable;
The operational period to be avoided is pⁿ = 1/ƒⁿ
RAO Amplification Factor (Aᶠ)
As with any dynamic system, such as high-speed Shafts, mode-shapes and vibrations, RAOs are subject to amplification that is affected by two primary factors:
1) non-dimensional frequency ratio (Ω)
and
2) damping ratio (ζ)
As can be seen in Fig 6, if the operational frequency of a vessel is close to its natural frequency (i.e. Ω = ƒ/ƒⁿ ≈ 1) and its damping ratio is low <0.56), it will induce a factor greater than '1'
i.e. a 3m wave amplitude will induce more than 3m movement in the vessel.
Note: ƒ = 1/p and ƒⁿ = 1/pⁿ {operational and natural frequencies are equal to the reciprocal of the operational and natural periods}
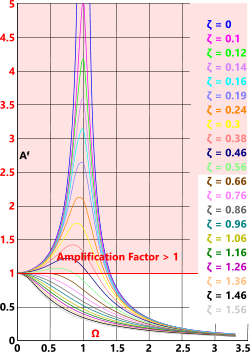
Fig 6. Amplification Factor
The above amplification is not generated by a single wave, but by repeated exposure to a series of waves of similar amplitude and frequency (Fig 6).
The factors governing this condition are the non-dimensional frequency and damping ratios as follows:
Heave: Ωz and ζz
Roll: ΩR and ζR
Pitch: ΩP and ζP
The damping ratio for Heave, for example is calculated thus:
ζ (vessel damping factor) = B33 ÷ ζᶜ
ζᶜ (critical damping factor) = 2√(C33.[m+A33])
where:
B33 (damping coefficient for heave) = ρ.g².A².Lᵥ ÷ ƒ³
A (radiation damping coefficient)
= 2.Sin(ƒ².Bᵥ ÷ 2g).exp(-[ƒ².Dᵥ ÷ g])
C33 (spring coefficient) = m.g ÷ Dᵥ
Lᵥ (vessel length)
Bᵥ (vessel beam)
Dᵥ (vessel draft)
m (vessel mass)
ρ (seawater density)
g (gravitational acceleration)
The only practical things you can do to modify a vessel's dynamic amplification factor are therefore as follows:
Alter the shape of its hull (Lᵥ, Bᵥ, Dᵥ) and/or its added mass (A33) and/or its operational frequency (ƒ).
Only a heading change (θ {ƒ}) or added mass coefficient (Ca {A33}) is likely to generate any noticeable reduction in amplification factor.
You will find that if you set the vessel heading (μ) to zero and its speed (v) to that of the wave (c), its heave will be equal to wave amplitude thereby reflecting the fact that the vessel is fully damped (ζz=1) under such conditions.
Response Amplitudes (RAs)
The responses calculated in RAO are not operators, i.e. you do not multiply them by the wave height or amplitude, they are actual (albeit theoretical).
Each response (Surge, Sway, Heave, Roll, Pitch and Yaw) is unique to the specified wave, the angle through it (θ) and the vessel's heading (μ).
Phase Lags
A phase lag is the angular delay that a vessel will respond to a wave amplitude at 'θ'
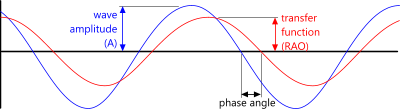
Fig 7. RAO Phase Angle
Negative phase lags mean that the vessel is responding before the wave peak passes its CofG (i.e. 'phase lead')
No phase lags are calculated for Surge, Sway and Yaw for the same reason as that provided for Added Mass above
Heave, Roll and Pitch calculated phase lags are not included in the associated response amplitudes.
RAO's phase lags can be entered into CalQlata's Vessacc where they will be incorporated into the displacements, velocities and accelerations at any point on a vessel's structure.
RAO Calculator – Technical Help
Whilst the output data can be used for any application, the RAO calculator has been specifically designed to work with Vessacc, which can import all but 3 of its required input data from RAO
However, as explained above (Response Amplitudes), the calculation results from this calculator apply only to the conditions entered. If you alter any of your input data (in RAO), your RA's will change. Please remember this fact when uploading your output from this calculator data into your Vessacc calculations.
Units
You may use any units you like for the input data as long as you are consistent. The output data will of course be in the same units. Example metric and Imperial units are provided in RAO's technical help pages.
Input Data
Wave Data (h, p, d), together with the angle through the wave (θ), define the conditions (L, t, k, ω, c, η) responsible for the response amplitude of the vessel. The wave form is calculated using the Linear theory.
Vessel Data
The velocity of the vessel (vᵥ) is in the positive 'xᴿᴬ' (Surge) direction
Dimensions (Lᵥ, Bᵥ) are to be taken at its water-line. The longitudinal distance to the CofG (Lᴳ) is measured from the aft end of the vessel at the water-line. Draft (Dᵥ), CofG (Hᴳ) and CofB (factor; Fᴮ) are all defined from the vessel's keel.
Fᴮ is a factor that represents the vertical position of the vessel's centre of buoyancy above its keel. For example: if a vessel's draft (Dᵥ) is 6m above its keel, and its centre of buoyancy (CofB) is 3.7m above its keel, this factor is calculated as follows; Fᴮ = 3.7 ÷ 6 = 0.617
The vessel's heading (μ) will define the frequency with which it encounters wave peaks and troughs. This angle may be any value between 0° (during which the vessel is travelling in the same direction as the wave) to 180° (during which the vessel is travelling in the opposite direction as the wave).
μ = 0° will mean that the wave encounter will be less frequent and should generate lower amplitude responses
μ = 180° will mean that the wave encounter will be more frequent and should generate greater amplitude responses
Output Data
Wave Data (L, t, k, ω, c, η) is provided for input to CalQlata's Vessacc calculator and information only.
RAs are calculated uncoupled and without the associated phase lags.
xᴿᴬ, yᴿᴬ & Yᴿᴬ are calculated as response amplitudes achieved at θ, there are no spring coefficients or damping effects included and they produce no phase lags
zᴿᴬ, Rᴿᴬ & Pᴿᴬ are calculated as response amplitudes achieved at θ and include the effects of added mass, damping and spring coefficients but do not include the associated phase lags
Phase lags (zᴾᴴ, Rᴾᴴ & Pᴾᴴ) are calculated for those response amplitudes that are subject to the effects of damping and spring coefficients.
Natural frequencies (ƒⁿz, ƒⁿR & ƒⁿP) are provided for those response amplitudes that are subject to the effects of damping and spring coefficients.
You calculate the natural periods thus; ƒⁿ = 1/pⁿ [seconds]
A damping ratio is calculated for heave (ξz), but you are required to provide one for both Roll and Pitch (ξR & ξP) see Data File below.
Metacentric heights (GMᵀ & GMᴸ) and righting arms (GZᵀ & GZᴸ) are calculated at θ and provided for information only.
Important Note
You may notice that the output values for heave zᴿᴬ, roll Rᴿᴬ and pitch Pᴿᴬ are greater than expected at the entered angle through the wave.
Such a result is due to the effect of your damping values that will induce an amplification factor if close to the natural frequency of the vessel.
To minimise this effect, you will need to reduce your added mass and drag coefficients and/or increase your damping ratios, which you will find in the datafile of the calculator.
This does of course mean that the values entered must reflect the design of your vessel.
Data File
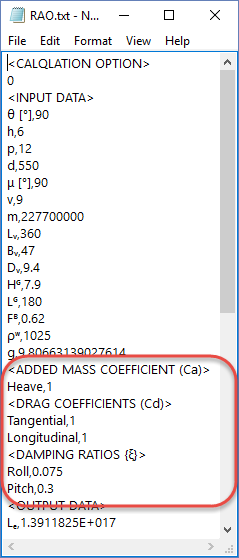
Fig 8. RAO Data File
Immediately below the 'input data' in the data file you will see the following variables (Fig 8):
Heave,1
Tangential,1
Longitudinal,1
Roll,0.075
Pitch,0.3
each of which may be altered according to your preferences.
Heave: if you enter a value of zero for Heave, A33 (added mass) will be calculated in RAO. Otherwise RAO will calculate the Heave added mass using the value you enter. This value is normally between 0.5 and 1.0. Sharp under-hull shapes will be closer to 0.5 and flat (or block) under-hull shapes will be closer to 1.0
Tangential & Longitudinal: you must enter values for both drag coefficients (Cd), which are normally between 0.5 and 1.0. Triangular hull sections will be closer to 0.5 and flat (or block) sided hulls will be closer to 1.0
Roll & Pitch: you must enter values for damping ratios (ξ). Roll is normally between 0.05 and 0.1 and that for Pitch is normally between 0.2 and 0.4
You alter the above variables as follows:
i) Save the calculation (menu item; 'File>Save Data')
ii) Open the data file (menu item; 'File>Open Data File')
iii) Scroll down to the appropriate heading '<ADDED MASS COEFFICIENT (Ca)>', <DRAG COEFFICIENTS (Cd)> or <DAMPING RATIOS {ξ}> and alter the value concerned taking care not to lose the comma (,)
iv) Save the data file
v) Load the data file into the calculator
(menu item; 'File>Load Data' or 'File>Quick Load' + click the Quick-Load link {Load Input Data})
vi) You may repeat the above procedure as many times as you wish; it is much quicker to use the Quick-Link if you wish to repeat this action a number of times
Exported Data
If this calculator and the vessel motions calculator are both installed on the same machine, you can import all RAO's data into Vessacc for automatic calculation minimising the work required and the opportunity for error. However, if you wish to change any of the imported data, you must do so in RAO, save the calculation, and reimport the modified results to Vessacc for accurate results.
Applicability
The RAO calculator is applicable to all floating objects and structures.
Accuracy
These calculations are theoretically accurate according to the classical theories involved, i.e. there is no margin of error, with the following provisos:
The values and formulas for Added Mass and Damping Coefficients are estimates proposed by various marine engineers over the years and these properties vary throughout any given cycle. CalQlata would suggest that within the Damping Ratio limits described above, our values should be within ±20% of actual values, however, they have greater effect on phase lags than response amplitudes.
Whilst these calculations may be correct, sea-states are not consistent and every following wave is different to every preceding wave; these calculations are therefore subject to the accuracy of nature itself, which is not always very predictable.
Further Reading
You will find further reading on this subject in reference publications(54)

