Ocean Wave Calculator
(hydrodynamic properties)
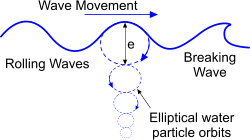
Fig 1. Ocean Wave Profile
Ocean (hydrodynamic) waves are produced as a result of an infusion of energy, either as a result of atmospheric winds or significant water body displacement from seismic events (earthquake, land-slip, etc.).
A wave is a series of rolling bodies of water moving in the direction of their roll. Their energy is transmitted down through the water depth in elliptical orbits, the eccentricity of which flattens with decreased water depth.
These rolling waves will remain largely intact whilst they are able to complete their uppermost elliptical cycle. Two conditions will disrupt this cycle and cause the wave to break:
1) Either the water depth is less than dimension 'e' in Fig 1; e.g. when an ocean wave reaches the shore.
The reason for a wave breaking 'forward and over' when it arrives at the shore is because the bottom of the elliptical roll is slowing down as it drags along the seabed whilst the top of the wave tries to keep going.
2) Or the wave is too high for its length and it becomes unstable⁽⁴⁾
Breaking Waves
According to Le Méhauté, a wave will break when the water depth is less than 0.78 of the wave height (Fig 4).
Whilst velocities and accelerations of rolling waves can be used directly in the designation of fluid forces in deep-water environments, this is not the case for breaking waves; the velocities and accelerations of which must be modified according to the type of breaking wave under consideration.
There are various types of breaking wave for which Galvin (1968) developed his parameter (β) that is based upon Ramón Iribarren Cavanillas' 'Iribarren number' (ξₒ = a / √[Hₒ/Lₒ]):
β = Hᴮ / a.g.T² = Hₒ / Lₒ.a²
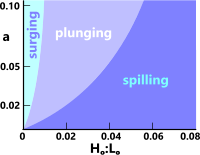
Fig 2. Ocean Wave Dimensions
spilling; β > 5
plunging; 0.1 < β < 5
collapsing; β ≈ 0.1
surging; β < 0.1
where:
a = the slope (or tangent) of the beach
Hᴮ = the height of the breaking wave
Hₒ = the deep-water wave height
Lₒ = the deep-water wave length
However, most theorists agree that this is not an exact science and that there is some overlap between the above categories.
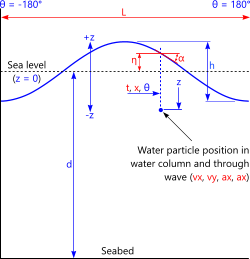
Fig 3. Ocean Wave Dimensions
From Fig 2 you can get an indication of the type of breaking wave to expect on a beach of a specified slope (a) from the wave's deep-water slope (Hₒ/Lₒ).
Walker (1974) suggested a celerity (wave speed) for the breaking wave of 1.25 x √[g.(d + ns)] (based upon the Froude number; 1 + ¼.H/d)
where; ns≈0 at breaking point leaving us with a wave speed of √(g.d).(1 + ¼.H/d)
The generally accepted theory for evaluating breaking waves is Dean's 'Stream Function', which whilst it is not included in the waves calculator, can be applied to horizontal water particle velocities for design purposes, as follows:
u = - √[g.d].γ₂/γ₁ . N∑n π.(n-2).Cosh{π.(n-2).γ₁.(d+z)/d} . [γn.Cos{θ.π.(n-2)} + (γn+1).Sin{θ.π.(n-2)}]
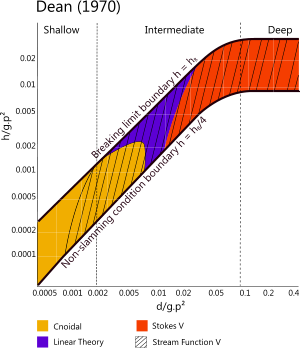
Fig 4. Theory Applicability
According to Dean (1970)
where:
Xn = unknown coefficient
g = gravitational acceleration
N = number of terms in the equation
n = term number (4,6,8,etc.)
γ₁ = d/L
γ₂ = H/L
γn = Xn / L.H.√(g/d)
d = water depth
H = wave height
L = wave length
θ = angle through wave (x/L - T/t)
x is distance through wave (L)
t is time through wave
T = wave period
Galvins parameter 'β' may be used to define the above unknown coefficient (Xn).
Ocean Waves Calculator - Technical Help
In the following sub-sections, you will see ocean wave calculation references to Depth, Height and Period which are given the variables 'd', 'h' and 'p' respectively (Fig 3, 'p' refers to the time associated with the passing of one full wave length; 'L')
As it can sometimes be challenging to match appropriate conditions to a theory⁽⁶⁾, example conditions for the above properties are provided in curly brackets '{}' for you to try. The ocean waves calculator will let you know if your input data falls outside the recommended parameter limitations for the selected theory in the two active display diagrams from Dean (Fig 4 for boundary conditions - wave slam) and Le Méhauté (Fig 5 for submerged conditions).
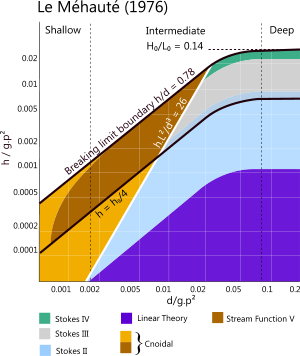
Fig 5. Theory Applicability
According to Le Méhauté (1976)
Units
You may use any units you like, but you must be consistent.
LINEAR (Airy)
Linear is the most robust theory and can be used for almost any calculation but is considered appropriate for sinusoidal profiles, i.e. small to medium rolling waves in deep water.
This theory is considered most appropriate if: L<2d and h/L<0.06 {Depth=1000, Height=5 & Period=12}
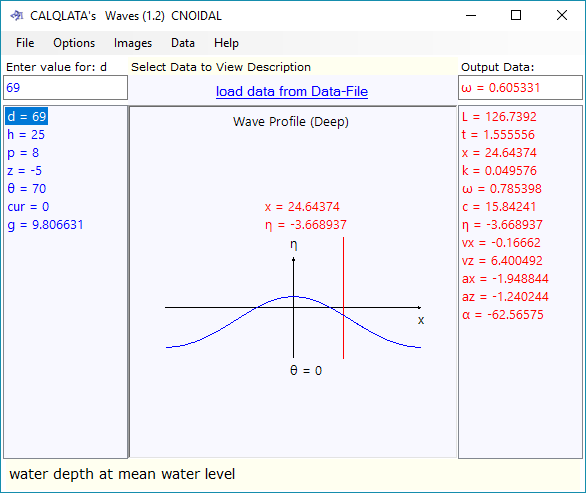
HYPERBOLIC & CNOIDAL
Hyperbolic theory is an alternative to Cnoidal and may be similarly applied to large waves in shallow water.
Whilst both Hyperbolic and Cnoidal wave length predictions are generally longer than other theories, the Hyperbolic theory predicts increasingly longer wave lengths as water depth increases given that wave Height and Period remain constant.
Of the two, Cnoidal is the most sensitive theory and applies principally to large waves in very shallow water and does not readily cope with inappropriate parameters.
Hyperbolic is considered applicable if: h/d>0.8 {e.g. Depth=20, Height=16 & Period=12}.
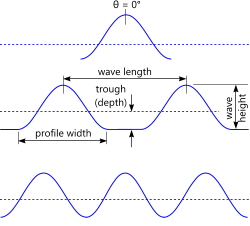
Fig 6. Limiting Cnoidal Wave Profiles
Cnoidal is considered applicable if: d/h≈2 and L>8d and h/(g.p²)<0.02 and d/(g.p²)<0.03
{e.g. Depth=45, Height=12 & Period=20}.
If the input parameters for a Cnoidal wave are too far from applicability, you will notice in the graphical representation of the wave that its entire profile begins to sink below mean water level (Fig 7). If you really need a result in deep water using this theory try increasing the period to say > 25 seconds.
Whilst Linear and the Stokes' waves follow continual profiles (η) as shown in Fig 3, i.e. the waves peak at 0° and 360° and the trough at 180°, in the case of shallow water, high waves and short periods the profile width of Cnoidal and Hyperbolic waves may be less than 360° resulting in flat water troughs (Fig 6)
A complete wave profile can be established by calculating and plotting 'η' for a selection of angles either side of θ=0°;
e.g. between -104° and 104°, where 104° represents the lowest point in the wave trough.
The width of a single wave is the horizontal distance between the lowest points of the wave profile where x = L.θ/2π
If 'x' is greater than L/2 these theories are not applicable for the input data used.
If 'x' is equal to L/2 these theories are applicable for the input data used and the train of waves will be continuous with no flat water at the troughs.
If 'x' is less than L/2 these theories are applicable for the input data used but the water level between wave profiles will be flat at trough depth (i.e. when η is minimum).
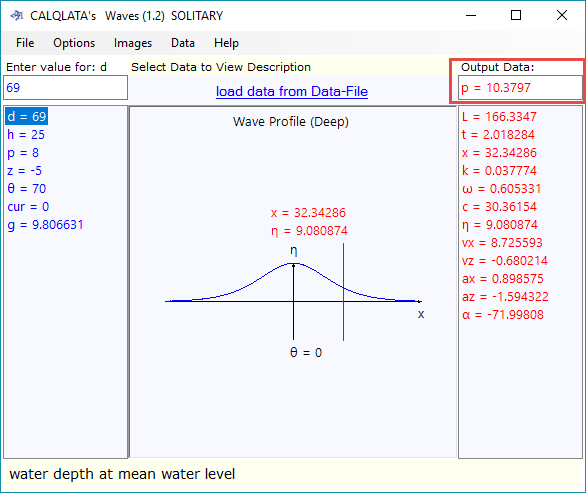
SOLITARY
Solitary wave theory applies to a single large rolling wave such as a tsunami or tidal wave. Almost any conditions can be considered applicable. The Period is calculated in this theory, so you will notice the calculated value appear in the 'Output Data' textbox with each new calculation (Fig 8). The input value, which is used for all other theories, remains visible in the input listing but has no effect on the calculation.
STOKES
Stokes' theories apply to ocean waves in deep water, with increasing Order applicable to increasing wave size: i.e. the lowest wave theory Order (STOKES II) applies to the smallest waves and the highest Order (STOKES V) applies to the largest waves (relative to water depth).
Stokes' theories are considered applicable if: L<8d with further qualifications for each Order:
STOKES II
Stokes II is considered applicable if: h/(g.P²)<0.008 and 0.002<d/(g.p²)
{e.g. Depth=300, Height=12 & Period=17}
STOKES III
Stokes III is considered applicable if: 0.008<h/(g.p²)<0.02 and 0.01<d/(g.P²)
{e.g. Depth=300, Height=19 & Period=15}
STOKES V
Stokes V is considered applicable if: 0.01<h/(g.p²)<0.05 and 0.01<d/(g.P²)
{e.g. Depth=300, Height=23 & Period=15}
Whilst Stokes V is generally used for extreme or design waves it is also used extensively in place of all Stokes' lower Order theories (II, III & IV).
Data Listing (water column)
Waves generates a list of horizontal and vertical velocities and accelerations (vx, vz, ax, az, ) through the wave (-180°<θ<180°) at elevation 'z' and through the water column at 'θ'.
Water column and wave length plots are divided into 360 divisions. Whilst the co-ordinates are provided for further processing, Waves also displays these plots in graphical form.
Notes
- A warning message 'Outside general conformance criteria for this theory' will appear if the input data does not fall within the applicability diagrams drawn up by Dean (Fig 4) and Le Méhauté (Fig 6), who respectively defined theoretical limits to wave boundary conditions and submerged conditions.
- Wave steepness is normally defined as h/L.
- Wave relative height is normally defined as h/d.
- The theories used in this software do not apply to breaking waves (refer to Figs 4 & 5) for definitions according to Dean and Le Méhauté.
- Where this software cannot handle your combination of parameters, you should consider Finite Element theories such as Stream function (for non-breaking waves) or those developed by Longuet-Higgins & Cokelet.
- Refer to Wind and Waves for wind velocity calculations and an assessment of the mathematical models.
Further Reading
You will find further reading on this subject in reference publications(6, 8 & 9)

