Logs and Trig Calculator
This logs and trig calculator is for standard mathematical tables including logarithms and plain/hyperbolic trigonometry functions.
Logs (logarithms)
Logs are useful for simplifying long multiplication and division hand calculations, which can be a tedious procedure and prone to error. It is much easier to add or subtract two numbers than to multiply or divide them. For example:
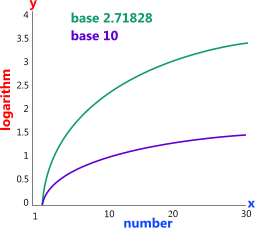
Fig 1. Number-Log Graph with Plain Axes
Multiply 12.75 by 145.23 and you get 1851.6825 or you could add together the logs of both (1.105510185 + 2.162056337), which gives you 3.267566522. The anti-log of this number is also 1851.6825
Divide the above numbers and you get 0.087791779 or you could subtract both logs (1.105510185 - 2.162056337) giving you -1.056546153. The anti-log of this number is also 0.087791779
Whilst both of the above examples have been carried out using logs to the Base 10, you can use any Base you like so long as the log and the anti-log have the same Base. The result will always be the same. The Base of a log simply describes the shape of a curve generated by a sequence of its values (Fig 1).
The multiplication relationship between log and anti-log of any two numbers (2 and 3 in this case) can be summarised thus:
(where e = the Log 'Base'):
Anti-Log: e² x e³ = e⁽²⁺³⁾
Log: Logₑ(2) + Logₑ(3) = Logₑ(2x3)
Note: The division (÷) relationship is exactly the same but the plus sign (+) should be replaced with a minus sign (-).
There is another function for logs, however. They frequently describe the relationship between two non-linear and co-dependent variables (e.g. x and y) and this relationship can often be attributed to a log (or anti-log) with a particular Base, allowing you to predict numerical associations (e.g. between x and y) mathematically.
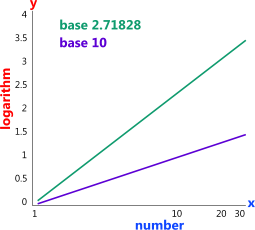
Fig 2. Log Graph with Plain Axis and Log Axis
As can be seen in Fig 1, plotting a number against its log using plain axes will produce a curve the shape of which will vary with its Base. In Fig 2 these same values are plotted on a graph of axes with the same limits, but with the x-axis set to a log scale which now shows the curves to be a straight line making the relationship linear and therefore much easier to predict unknown relationships between 'x' and 'y'. Whilst the Base of the x-axis in Fig 2 is '10' it can be seen that the natural log (Base 2.71828) curve is also a straight line when plotted on this graph, it simply has a different slope. In fact you can set your axes to any log Base and any log relationship between x & y will always be linear, the curves will simply have different slopes.
Some relationships are stated as being 'Log-Log' meaning that the log of 'x' is related to the log of 'y', either of which can have any base, examples of which can be seen in Fig 3 & 4 of the Waves technical help page. The curve of any such relationship will always be linear (a straight line) whether the axes are plain or log but they must be both the same (plain-plain or log-log). However, if both axes have log scales but different bases, the curve will not be a straight line.
You can find the power of a number in an equation by using logs, thus:
Xn = Y
n = Log(Y)/Log(X)
Trig (trigonometric) Functions
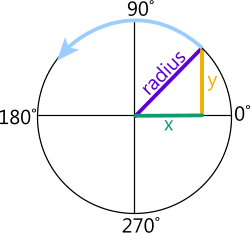
Fig 3. Circular Trig Origins
A trigonometric function is primarily a number that describes the non-linear relationship between the 'x' and 'y' co-ordinates of a point 'P' on the circumference of a circle (Fig 3). However, because the radius of the circle is also the hypotenuse of a right-angled triangle (formed by the radius and its 'x,y' co-ordinates), these trigonometric functions can also be used to resolve the unknown properties of a triangle.
The Sine, Cosine and Tangent functions are all slopes of the radius (or hypotenuse) and therefore calculated by dividing one side of the triangle by another:
The Sine is the slope determined by dividing the 'y' co-ordinate (the numerator) by the radius (the denominator)
The Cosine is the slope determined by dividing the 'x' co-ordinate (the numerator) by the radius (the denominator)
The Tangent is the slope determined by dividing the 'y' co-ordinate (the numerator) by the 'x' co-ordinate (the denominator)
The reason why Sine and Cosine vary between 0 and 1 is because the denominator is the radius. It doesn't vary in length and is always larger than the numerator (the 'x' or 'y' co-ordinate). The reason why Tangent varies between 0 and infinity is because the numerator ('y') and the denominator ('x') both vary in length as the point passes around the circumference of the circle. As the radius approaches 90° the denominator ('x') tends towards zero length. Any number divided by zero is infinity.
The trigonometric functions alternate between positive and negative values as the axes change polarity (sign) and the point travels around the circumference. For example, we can follow the polarity of each function around 360° by looking at their equations in each quadrant (Fig 3 & 4):
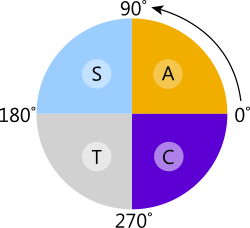
Fig 4. Positive Trig Functions
Quadrant 'A': Sine = +y ÷ +radius so the result will be positive
Quadrant 'S': Sine = +y ÷ +radius so the result will be positive
Quadrant 'T': Sine = -y ÷ +radius so the result will be negative
Quadrant 'C': Sine = -y ÷ +radius so the result will be negative
Quadrant 'A': Cosine = +x ÷ +radius so the result will be positive
Quadrant 'S': Cosine = -x ÷ +radius so the result will be negative
Quadrant 'T': Cosine = -x ÷ +radius so the result will be negative
Quadrant 'C': Cosine = +x ÷ +radius so the result will be positive
Quadrant 'A': Tangent = +y ÷ +x so the result will be positive
Quadrant 'S': Tangent = +y ÷ -x so the result will be negative
Quadrant 'T': Tangent = -y ÷ -x so the result will be positive
Quadrant 'C': Tangent = -y ÷ +x so the result will be negative
The quadrants can therefore be labelled to designate the positive functions in each:
Quadrant 'A' = 'All' (all functions are positive)
Quadrant 'S' = 'Sine' (the Sine function is positive)
Quadrant 'T' = 'Tangent' (the Tangent function is positive)
Quadrant 'C' = 'Cosine' (the Cosine function is positive)
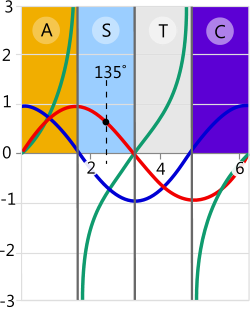
Fig 5. Sin, Cos, Tan Plots on Linear Graph
This diagram (Fig 4) is generally referred to as the CAST diagram to help you to remember the positive and the negative functions.
Fig 5 shows the three principal trigonometrical plots (Sine, Cosine & Tangent) between 0° and 360° (0 to 6.2 radians) translated into a straight-line graph. The letters A,C,S & T refer to the quadrants described in Fig 4.
As can be seen in Fig 5, the Sine (Sin) and Cosine (Cos) plots are exactly the same shape but 90° out of phase. This is to be expected as the 'x' and 'y' axes have exactly the same minimum and maximum length but vary in opposite directions as the point passes around the circumference.
Fig 5 also shows the plot of the Tangent (Tan) function going to infinity as the point approaches 90° (1.57 radians) and 270° (4.71 radians). This is because whilst the 'y' co-ordinate never exceeds the radius in length, the 'x' co-ordinate at these two positions becomes infinitely small, so the Tangent equation 'y÷x' will result in an infinitely large value.
Should you wish to find the slope of any of these functions (Fig 5) all you need to do is work out its derivative at the angle required. For example, the slope of the Sine curve at 135° is calculated thus; x = 135°, dy/dx = Cos(x)⁽¹⁾, Cos(135°) = -0.707106781. As you can see in Fig 5, the slope is indeed negative (going down from left to right) and at 45° (0.7071 radians)!
Hyperbolic Trig Functions
These functions are not for the resolution of angles. They are simply physical relationships closely related to a combination of exponential (eⁿ) and trigonometric functions that frequently occur in nature⁽¹⁾, such as hydrodynamic waves (see Waves technical help page on this website).
Logs and Trig Calculator - Technical Help
Logs (logarithms) ⁽²⁾
You may select the common or natural logarithm Base from the 'Base' drop-box or type in any other value you prefer. However, if you delete the 'Base' value or enter a zero, the logs and trig calculator will automatically insert the value 10. LogTrig automatically defaults to the common log Base of 10 if it doesn't recognise the entered value.
Trig (trigonometric) and Hyperbolic Functions ⁽²⁾
When entering an angle to find its trigonometric function, you select 'radians' or 'degrees' from the input data drop-box and whatever you enter will be automatically converted and inserted into the other input data item. For example: if you enter a 'radian' value, it will be automatically converted into degrees and inserted into the 'degrees' drop-box slot, and vice-versa.
Output Data
LogTrig will let you know if an obvious error has occurred. If, however, you get 'NaN' or 'infinity' you should check for incorrect input data or unacceptable zeros.
Notes
- CalQlata has provided numerous derivatives of hyperbolic trigonometric functions, including many worked examples, on the 'Useful Formulas – Differentiation Trig' page on this website.
- If you enter an input value that doesn't compute for any of the six listed results, the logs and trig calculator will display an output value of '0E+000' followed by; '#' for the functions concerned.
Further Reading
You will find further reading on this subject in reference publications(3 & 12)

