Piling Calculator
(tubular steel anchor & foundation)
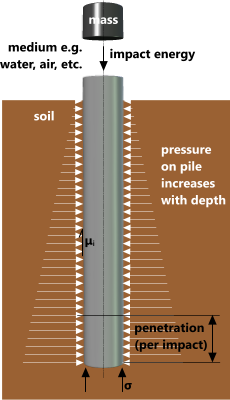
Fig 1. Pile Installation Resistance
Piles are used; as anchors, to raise structures above ground or to prevent movement (subsidence) in structural foundations. They can be solid concrete or tubular steel depending upon application.
Concrete piles normally support very large vertical compression loads and are installed/manufactured by digging a hole in the ground into which a pre-fabricated pile is lowered and subsequently buried or into which uncured concrete is poured. These piles are not covered by CalQlata's piling calculator.
Hollow, tubular steel piles, which are the subject of CalQlata's piling calculator, are generally used as anchors or to prevent movement in small to medium structural foundations in suspect soil conditions either on land or in the seabed.
Soil
Prior to 450m years ago the earth's surface was rock; there was no soil anywhere. Since then, soil has accumulated over most of its surface from decomposed vegetable and animal matter and eroded rocks. Soils vary widely in composition and character dependent upon numerous variables, such as; composition, temperature and water content.
Sources of soil properties differ widely, not because they are incorrect but simply because they are all different. It is therefore always a good idea to test soil in the location to be piled with a small diameter pin, penetrating to a depth suitable for the desired level of confidence. This is a relatively inexpensive and reliable method of preparation for pile sizing prior to installation. The same calculation techniques may be applied to the pin as those for the pile.
Specified soil bearing strengths are only valid under precise conditions; depth, voids, entrained water, rock particles (stones), composition, temperature, etc. all contribute to variations in strength over very small volumes. Moreover, bearing strength normally varies with load magnitude and direction, i.e. it will significantly reduce when loaded in tension or compression near the surface.
Because soil strength increases with depth, lateral pressure from the soil on the pile wall is conservatively assumed by CalQlata to be equal to the pressure at depth multiplied by the Poisson's ratio of the soil (as opposed to its shear angle, which may also vary with depth).
Resistance to a compression force at the base or tip of the pile (Fig 1), that generates incremental penetration (δd), should normally be equal to the Combined Stress in the soil at depth. However, because conditions at the tip of a pile are variable and largely unknown⁽¹⁾ during installation, the piling calculator conservatively uses bearing strength alone when calculating for pile tip impact resistance.
Pile Installation
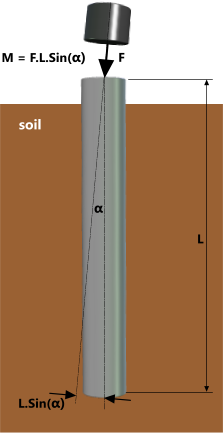
Fig 2. Pile Misalignment Moment
Fig 1 shows the resistance forces for a typical steel tubular pile during installation.
Piles are normally hammered into the ground by dropping a heavy weight onto them from a specified height. The impact force is generated from the potential energy in the mass. If the hammer is dropped in a dense medium, such as water, its effective mass (mₑ) must be used in the impact energy calculations (see Input Data below).
Frictional resistance⁽²⁾ between the soil and the pile's internal and external vertical surfaces increases with depth. Incremental penetration is achieved by overcoming bearing stress in the soil over the surface area of the tip of the pile wall. The force generated by the impact energy, which varies with each incremental change in soil penetration, must be sufficient to overcome both of these loads.
As pile depth increases, more of the impact force is lost in overcoming increased frictional resistance, reducing the force available for penetration. As such, incremental penetration decreases with installed depth, which increases the force on the pile with each impact.
It is unlikely that soil will have the same bearing strength, resistance to shear, friction coefficient and Poisson's ratio all the way down to the installed depth, therefore it is unlikely that each impact will generate the expected penetration at the depth concerned.
Whilst it is reasonable to continue piling until the impact force (F) is sufficient for your needs (Ŵ < F < W̌) it would be wise to ensure that the final value (F) is greater than (Ŵ+W̌)/2
The force (F) for each impact is provided in the piling calculator.
Pile strength
The pile wall must be capable of withstanding installation and operational loads and separate calculations are required to establish pile integrity based upon your specific design conditions. The most likely cause of pile failure, however, is wall-disruption during installation.
Disruption or collapse of the pile wall is due to excessive membrane stress from hammer/pile misalignment (Fig 2), a reasonably conservative estimate of which can be found using the following flat-plate formula: σỵ = 6.M/t
There are many formulas for addressing pile strength under compression some of which involve classical or elaborate formulas all of which can be reliably predicted using the Euler-Rankine column buckling calculation in which you add the Youngs modulus of the pile material to that of the soil (Eᵖ+Eˢ) when generating a composite stiffness (EI) for the column.
Pile Design Capacity
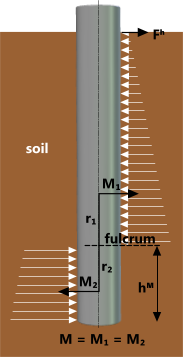
Fig 3. Lateral Capacity
Weight is resisted by a combination of frictional resistance and soil bearing strength. Horizontal loads must be opposed by lateral compression in the soil that varies with depth, composition and density. Tensile loads from anchors are resisted by the mass of the pile plus the soil plug if it remains internally contained and any residual friction between the soil and the pile wall.
As with all theoretical interpretations of practical problems, there is a certain degree of estimation in the final result.
For example:
Horizontal Force: Resistance to horizontal loads produces a moment couple (M) at height 'hᴹ' (Fig 3), the magnitude of which is due to a combination of soil bearing strength and pressure @ depth. Bearing strength is not the same when loaded horizontally as it is when under compression due to lift towards the surface, moreover, pressure generates greater resistance to horizontal forces than bearing strength at significant depths (i.e. when density x depth > bearing strength). Therefore, CalQlata has ignored the effects of bearing strength for horizontal loads in the piling calculator and assumed a lateral resistance based upon pressure x depth⁽⁴⁾. You will need to verify that your pile does not flatten just below the soil surface as a result of the horizontal force.
Compression Force: Unless a pile is penetrated to underlying rock, its carrying capacity (Fig 4; W) will be dependent upon the frictional resistance and bearing capacity of the soil that may or may not be consistent with surface conditions. In which case, you could base the carrying capacity of the installed pile on the final impact force. It would be wise, however, to apply a suitable safety margin to account for potential creep. CalQlata's rule of thumb is to assume full bearing capacity and ⅔ of the frictional resistance (R̂ᵛ). The piling calculator provides both theoretical (W̌) and rule-of-thumb (Ŵ) values in its output data.
Combined Force: When piles are subject to combined vertical and horizontal loads (Fig 5; W), frictional resistance from the vertical component will be reduced if the horizontal component is sufficient to overcome strain in the soil. If the soil and the pile lose contact over 50% of its external surface area frictional resistance should be ignored. Vertical upwards resistance will be due only to weight (pile and soil plug if retained) and compression resistance will be due only to bearing stress (σ) at the tip of the pile.
Caution
Whilst the frictional resistance in a pile may be included in the pile bearing capacity, care should be taken to ensure the following are accounted for during its design life:
1) A measure of creep can occur over time due to inconsistences in the soil through strata-variation and vibrational loads
2) Settlement may result in the pile creeping into a low strength stratum
3) Underground water will reduce frictional resistance and bearing strength
4) Rock that is partially supporting the pile may induce tilt over time
5) Deformation of the pile wall during installation may lead to collapse during operation
All of the above can be accommodated with suitable soil tests to a depth beyond the anticipated pile depth.
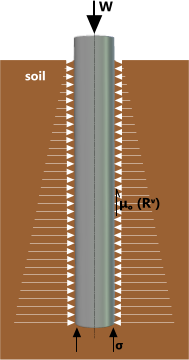
Fig 4. Axial Capacity
Piling Calculator - Technical Help
Units
You may use any units you like, but you must be consistent.
The input value for gravitational acceleration (g) is used only to convert the impact energy into a mass-force.
Installation
The piling calculator applies a horizontal pressure (that varies linearly with depth) to the internal and external pile wall due to the soil's Poisson ratio. Resistance to incremental penetration is calculated using only the bearing stress (σ) of the soil, shear stress (τ) is used to calculate the shear angle for horizontal force (F̌ʰ).
Design Capacity
The piling calculator provides numerous design loads, only the minimum values of which (R̂ᵛ, F̂ᵛ, Ŵ) can be used with high confidence and no proof-testing. If you wish to rely on higher design capacities than these, it is advisable to conduct suitable time-dependent loading tests.
Variable Strata
Unless you wish to carry out detailed calculations for each variable layer (Fig 6), you may conservatively assume your pile is only as deep as the sum of the thicknesses of the high-strength layers, ignoring the effect of low-strength layers altogether. This is also a more accurate approach than assuming average soil properties over the actual depth.
Input Data
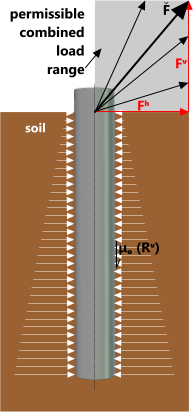
Fig 5. Combined Forces
D = maximum required pile depth
Øᵢ = pile inside diameter
Øₒ = pile outside diameter
ρᵐ = medium density⁽³⁾
ρʰ = hammer density⁽³⁾
ρᵖ = pile density
ρˢ = soil density
m = hammer mass⁽³⁾
hᵈ = drop height
σ = soil bearing stress
τ = soil shear stress
μᵢ = coefficient of friction during installation⁽²⁾
μₒ = coefficient of friction during operation⁽²⁾
ν = Poisson's ratio (soil)
Output Data
mₑ = effective hammer mass⁽³⁾
E = impact energy
A = pile wall cross-sectional area (tip)
Ď = total maximum depth (d + δd after final hit)
n = number of hits (to achieve Ď)
R̂ᵛ = minimum vertical frictional resistance during installation⁽⁵⁾ (due to μᵢ)
Řᵛ = maximum vertical frictional resistance after settlement⁽⁵⁾ (due to μₒ)
F̌ʰ = maximum horizontal force (at soil surface)
F̂ᵛ = minimum pile lift force (pile mass only)
F̌ᵛ = maximum pile lift force (including mass of plug and Řᵛ)
Ŵ = minimum weight carrying capacity (from; ⅔μₒ + σ)
W̌ = maximum weight carrying capacity (from; μₒ + σ)
hᴹ = height from pile tip to fulcrum
r₁ = moment arm above fulcrum (for information only)
r₂ = moment arm below fulcrum (for information only)
M₁ = Moment above fulcrum⁽⁶⁾ (for information only)
M₂ = Moment below fulcrum⁽⁶⁾ (for information only)
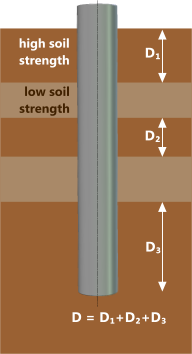
Fig 6. Variable Soil Strata
Hit Sequence Results:
N° = impact number
δd = impact depth
d = total depth after impact
F = force of impact
See Material Properties below for some represenative material properties.
Material Properties
Installation Medium: If your pile is installed by a hammer dropped under water you should enter a medium density (ρᵐ) for water, otherwise you should enter a value for air or set this value to zero.
Hammer material: The density of the hammer material (ρʰ) is reduced by the medium density in the calculation (ρᵐ) for the impact energy (E) calculation. It is therefore important that both densities are representative
Pile Material: The density of the pile material is only used in the calculations for the force required to pull the pile out of the ground (Fᵛ)
Soil Material: The properties of the soil should be based upon site-test values if at all possible. This can be established by inserting a pin into the ground at the site of the pile and then retrospectively establishing the properties of the soil conditions using the pile calculator and modifying the soil properties (σ, μᵢ & μₒ) ensuring that:
a) The retrospective calculations reflect the actual conditions during installation, and;
b) The extraction loads are measured after at least 30 days of settlement. Alternatively, the following data may be used for estimation purposes:
| Densities | Substance | kg/m³ | lb/in³ |
|---|---|---|---|
| ρᵐ | air | 1.256 | 4.54E-5 |
| water | 1000 | 0.0361 | |
| seawater | 1023 | 0.037 | |
| ρʰ | steel | 7850 | 0.2836 |
| concrete | 2400 | 0.0867 | |
| granite rock | 2750 | 0.09935 | |
| ρᵖ | steel | 7850 | 0.2836 |
| aluminium | 2685 | 0.097 | |
| titanium (HT) | 4456 | 0.161 | |
| stainless 316 | 7941 | 0.2869 | |
| ρˢ | clay-dry | 1590 | 0.0574 |
| clay-medium | 1625 | 0.0587 | |
| clay-wet | 1750 | 0.0632 | |
| loam | 1275 | 0.0461 | |
| silt-dry | 1920 | 120 | |
| silt-wet | 2163 | 135 | |
| sand-dry | 1600 | 0.0578 | |
| sand-wet | 1900 | 0.0686 |
| Stress | Substance | kg/m² | lb/in² | ν |
|---|---|---|---|---|
| σˢ | clay-dense | 35 to 55 | 0.05 to 0.08 | 0.45 |
| clay-medium | 20 to 35 | 0.03 to 0.05 | 0.35 | |
| clay-loose | 10 to 20 | 0.014 to 0.03 | 0.3 | |
| loam | 7.5 to 15 | 0.01 to 0.02 | 0.3 | |
| silt-dense | 4.5 to 7.5 | 0.0064 to 0.01 | 0.35 | |
| silt-loose | 1 to 4.5 | 0.001 to 0.0064 | 0.3 | |
| sand-dry | 10 to 30 | 0.014 to 0.04 | 0.4 | |
| sand-wet | 5 to 10 | 0.007 to 0.014 | 0.3 | |
| τˢ | clay-dense | 29.4 to 46.2 | 0.0418 to 0.0656 | |
| clay-medium | 11.5 to 20.2 | 0.0164 to 0.0287 | ||
| clay-loose | 3.6 to 7.3 | 0.0052 to 0.0104 | ||
| loam | 4.3 to 8.7 | 0.0062 to 0.0123 | ||
| silt-dense | 0.8 to 1.3 | 0.0011 to 0.0019 | ||
| silt-loose | 0.1 to 0.4 | 0.0001 to 0.0006 | ||
| sand-dry | 8.4 to 25.2 | 0.0119 to 0.0358 | ||
| sand-wet | 2.9 to 5.8 | 0.0041 to 0.0082 |
| Substance | μᵢ | μₒ |
|---|---|---|
| clay-dense | 0.225 | 0.45 |
| clay-medium | 0.2 | 0.4 |
| clay-loose | 0.15 | 0.3 |
| loam | 0.175 | 0.35 |
| silt-dense | 0.15 | 0.3 |
| silt-loose | 0.125 | 0.25 |
| sand-dry | 0.1 | 0.2 |
| sand-wet | 0.175 | 0.35 |
Applicability
The pile calculator only applies to tubular piles embedded into surface soil
Accuracy
The calculations in the pile calculator are only as accurate as the information entered. The output data is based to a large extent on pressure varying linearly with depth and consistent soil density over this depth. Where this is the case, the results are expected to be within ±10% of actual values.
Where soil variability occurs over the depth of the pile, average values should be used for soil properties, in which case; results are expected to be within ±20% of actual values.
It is highly unlikely that any piling calculation will achieve significantly greater accuracy than the above expectations.
Notes
- Impact vibration, soil displacement and variable conditions with depth all vary the end load of a pile during installation in an uncontrolled manner
- Frictional resistance is less during installation than operation due to settlement (after ≈30 days). CalQlata recommends that, unless exact values are known, a friction coefficient for cohesive soils during installation should half that for operation, which is normally ≈0.35. For non-cohesive soils, both values should be assumed the same at ≈0.15
- Impact energy uses effective hammer mass mₑ = m.(ρʰ-ρᵐ)/ρʰ
- Lateral load on the pile walls is calculated using formula ν.d.ρˢ
- Including internal and external vertical walls of the pile
- This information is provided as a check: M₁ should be identical to M₂ if the calculation is correct
Further Reading
You will find further reading on this subject in reference publications(8, 9, 51 & 52)

