Combined Stress Calculator
(incl. principal & equivalent)
Note: Refer to Figs 2 & 3 for stress type colour coding.
Combining stresses is simply the conversion of six different stresses (three primary and three shear) at a common location into more convenient equivalent values.
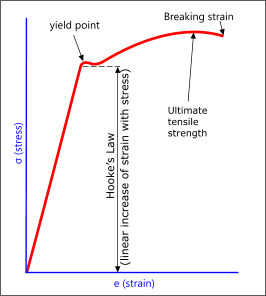
Fig 1. Stress-Strain Curve for Metals
The conversion into Principal stresses (see Principal Stress below) is for use in fatigue calculations (see CalQlata's Fatigue calculator).
The conversion into an equivalent stress (see Equivalent Stress below) is for use in extreme design conditions.
Elastic Stress
As most users of this calculator will be aware, stress is measured in load per unit area, which, in most metals, results in a deformation (strain) that varies linearly (elastic strain) with increasing force over the same area. This linear deformation will continue to increase until the material reaches its yield point, after which, the material will deform non-linearly (plastic strain) and ultimately break (Fig 1 - see Plastic Stress in Beams).
The slope of the graph produced by the 'Hooke's law' region (Fig 1) is called the Young's modulus of the material and usually retains the same slope even after heat treatment or work hardening, although the yield point may well rise or fall.
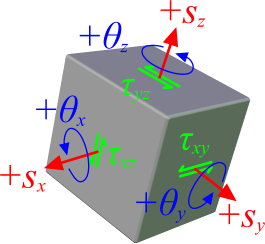
Fig 2. 3-D Stress-Strain Relationships
Stresses are generated at any point in a material in three primary directions; x, y, & z according to the Right-Hand rule. These are called the Primary stresses (Fig 2).
Shear stresses (tearing action through the 2-D plane at right-angles to the primary stress) are automatically generated as a consequence of Poisson's ratio and bulk modulus, which occurs when a material's cross section area reduces as it increases in length with increased load (i.e. volume does not change).
Shear stresses can also be generated directly by twisting or slipping the material (like a pack of cards). Calculations in this calculator are only valid if all the primary and shear stresses in your material obey Hooke's law.
Plastic Stress
Whilst it is usually damaging for a material to reach or exceed its yield stress, this may not always be the case. Where a material has exceeded yield and remains in service its properties will have changed and the yield stress will be different owing to work hardening, but this is not a subject for discussion here (see CalQlata's ElastiPlast calculator).
Principal Stress & Direction Cosines
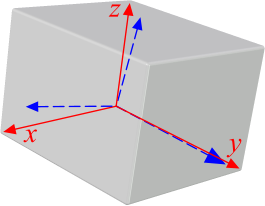
Fig 3. Rotation of Primary>Principal Stresses
The three coincident principal stresses (see Fig 3) in an elastic material are the three primary stresses rotated through their three primary axes and increased in magnitude to take into account the effect of the associated shear stresses (Fig 2). Combined Stress also provides the cosine values of these rotations.
Principal stresses should always be used in the evaluation of material fatigue life.
Equivalent Stress
In addition to the Principal stresses and their Cosines, Combined Stress also calculates the 'Equivalent' stress, a value that is regarded as a single stress equivalent to all three Primary and all three Shear stresses.
St Venant believed that strain rather than stress is the reason for material failure. Therefore Combined Stress also provides a value for St Venant's Equivalent stress, which is based upon strain energy, just in case you prefer this method.
Equivalent stresses are used as a guide to the combined effect of all the stresses in a material.
Combined Stress Calculator - Technical Help
Units
You may use any units you like, but you must be consistent.
Self-Check
The equivalent stress can be calculated in two ways, by using;
1) Von-Mises' formula which reaches the final value directly from the Primary and Shear stresses, and;
2) polynomial solution via the principal stresses.
Both of which are completely different calculation methods.
By way of an internal check, Combined Stress calculates the equivalent stress using both the above mentioned techniques (1) Von Mises & 2) polynomial). If they're equal the principal stresses must be correct.
Data Import
Combined Stress provides a data import facility for you to extract information from Pipe if it has been installed.
The information retrieved from Pipe is the three primary stresses (sx, sy and sz), the three shear stresses (τxy, τxz and τyz) and Poisson's ratio (ν).
Further Reading
You will find further reading on this subject in reference publications(1, 4 & 10)

