Plastic Strain in Metals

Fig 1. Slip Planes in a Metal Crystal
All the atoms in a perfect metal crystal will be packed together in their natural lattice structure. In this state, the crystal will represent the metal concerned in its lowest energy condition. It will be at its softest and most flexible.
Theoretical elastic deformation (Fig 1) of a metal crystal will mean that all the atoms will move relative to each other such that subsequent release of the stress generating this deformation will allow all of the atoms to return to their pre-stressed position and state. In theory, this stress can be applied and released continuously with no effect on the metal’s physical properties or the crystal structure.
Plastic deformation (Fig 1) is the permanent slipping of planes of metal atoms within this lattice structure, whereby the release of the applied stress will result in a permanent deformation of the crystal. I.e. the atoms cannot return to their pre-stressed location within the crystal. In theory this slippage could still result in a perfect crystal of a different shape. In practice, however, this process almost always results in the generation of smaller crystals.
The more this deformation occurs, both in frequency and magnitude, the smaller the composite crystals will become. If foreign atoms, such as carbon are introduced into an iron crystal, the smaller crystals will remain in place as the foreign atoms will sit in the gaps between the small crystals maintaining the structure. The greater the quantity of foreign atoms introduced, the smaller the individual crystals and the more brittle the material becomes.
Yield Stress
For most metals, there is a minimum stress magnitude that is needed to force the atomic planes to slip; i.e. deform plastically, and below which the atoms will (largely) return to their original position (prior to deformation). This magnitude is called the yield stress for the metal (Fig 2; y).
Ultimate Tensile Stress
During the deformation process at stresses greater than yield, the metal will increase in strength due to work-hardening, which continues until reaching its ultimate tensile strength (Fig 2; u) and after which the metal will suffer internal fracturing until it breaks (Fig 2; b).
Work Hardening
In theory, work hardening a metal will reproduce exactly the same stress-strain relationship as in its natural state but pushed up and to the right (Fig 2; r-w-u-b) based upon the stress applied above yield, generating a residual stress in the metal (Fig 2; σr) at rest and reducing its strain capacity (Fig 2; eb-ey).
This theoretical relationship is difficult to achieve in practice, however, as applied stresses throughout a metal body are rarely consistent.
Stress-Strain Relationship
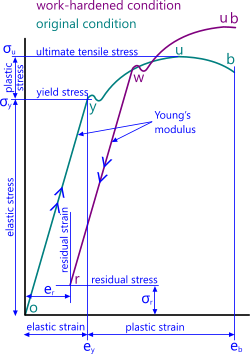
Fig 2. Stress and Strain in Metals
Metals normally respond to stress in a way similar to that shown in Fig 2. In that they obey Hooke's law up to an elastic limit ('y') and above which the material will deform plastically (permanently) but will relax according to its Young's modulus relationship leaving a residual stress (and strain) in the material.
Plastic stress doesn’t have to be damaging to a metal (e.g. steel), it only becomes plastic or behaves plastically whilst it is being deformed. Once this stress is released the metal will relax elastically to the condition shown at point 'r' in Fig 2 but with a residual stress (σᵣ) and strain (eᵣ).
This process is called ‘work hardening’ whereby the metal will be harder, have a higher minimum yield and a higher ultimate tensile stress as shown by plot 'r-w-u-b' in Fig 2. In practice, however, the process of work hardening, which reduces grain size, also makes the material more brittle reducing its ability to neck before failure (Fig 2; 'u-b') thereby reducing the available failure safety margin beyond ultimate tensile stress.
Beam Bending
When a beam or plate is bent plastically, it doesn’t mean that the entire section is being deformed plastically. As deformation increases, the outer layer of a deformed beam will become plastic whilst the innermost section remains elastic. Fig 3 shows the sequence of events from a fully elastic bending condition to a plastic hinge, which is when the two outer layers of plastically deformed material converge. If the beam continues to bend after achieving a plastic hinge it will very soon afterwards tear in the region of tensile deformation (the outside of the bend; Fig 3). It is inadvisable to allow a beam or plate to bend beyond its plastic hinge condition even in ultimate Limit-State Design conditions.
Theory vs Practice
The difference between the ‘theoretical’ and ‘practical’ plastic stress conditions in Fig 3 are that; in 'theory' the shape of the section remains the same during bending whereas in ‘practice’ it alters (Fig 4). The outer layer of plastic deformation, which is under tension, will stretch and flatten reducing the cross-sectional area, whereas the inner layer of plastic deformation will become larger as it compresses pushing the elastic layer and the neutral axis towards the outside of the beam bend radius.
Limit-State Design
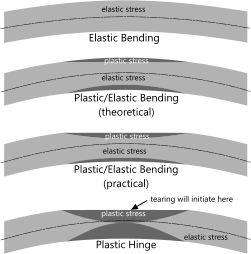
Fig 3. Extreme Bending in Metal Beams
Limit state design is used to determine the limiting condition of a structure under extreme or design conditions, such as serviceability, fatigue, accidental and ultimate. Whilst it is acceptable to design a structure that will deform plastically under ultimate limit state conditions, it is only acceptable if the integrity of the structure remains intact. Deformation in any member that generates a plastic hinge (or worse) cannot be considered to be intact.
Plastic stresses should never be allowed to occur in serviceability or fatigue limit state design scenarios.
Poisson’s Ratio
Poisson’s ratio for steel increases (jumps) from ≈0.3 during elastic deformation to almost 0.5 under plastic stress (Fig 4)
Plastic Stress Calculator - Technical Help
As the change in shape under plastic deformation is difficult to control and therefore predict, the calculations in the plastic stress calculator assume a theoretical shape for each section included, i.e. the cross-sectional shape does not change under plastic deformation (Fig 5; see Theory vs Practice above). This will result in an optimistic bending moment prediction.
The plastic stress calculator also assumes the stress applied to the plastic region of the beam is mid-way between the yield stress of the material and its ultimate tensile stress, which is highly likely in the case of a plastic hinge, however, anything less than a plastic hinge should result in a slightly reduced average plastic stress.
Units
You may use any units you like, but you must be consistent.
Plastic Strain in ElastiPlast
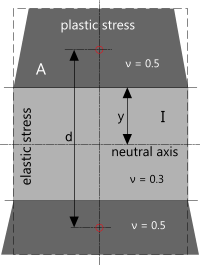
Fig 4. Sectional Variations
The plastic stress (σp) used in ElastiPlast is calculated as follows: σp = (σy + σu)÷2
If you would like to increase σp, you should multiply the ultimate tensile stress (σu) by the following factor ('F') where 'G' is the amount by which you would like to increase σp:
F = 1 + G.(σy/σu + 1)
e.g. if you want to increase σp by 20% then you multiply σu by 1 + 0.2x(σy/σu + 1) {i.e. 1.3424}
If you would like to decrease σp, you should multiply the ultimate tensile stress (σu) by the following factor ('F') where 'G' is the amount by which you would like to increase σp:
F = 1 - G.(σy/σu + 1)
e.g. if you want to decrease σp by 10% then you multiply σu by 1 + -0.1x(σy/σu + 1) {i.e. 0.829}
If you change the value of σu, however, the same modified σp will also apply to the plastic hinge bending moment (M̌) calculation.
In addition to the two extreme bending moments for a beam under plastic-stress (M̂ for yield stress in the outside fibres and M̌ for a plastic hinge), ElastiPlast also calculates the bending moment (M) required to position the elastic limit 'y' above (and below) the neutral axis; comprising the bending moment in the elastically deformed section (Me) and the bending moment in the plastically deformed section (Mp), i.e. M = Me + Mp
Applicability
This calculator applies only to the beam sections included and materials that follow a stress-strain relationship similar to that shown in Fig 2, i.e. early deformation obeys Hooke’s law after which, the material deforms plastically.
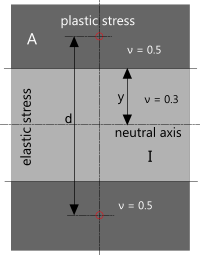
Fig 5. Sectional Stability
Accuracy
If a value of 'y' is entered outside the beam section, the result for 'M' will be unreliable.
If a value of 'σy' is entered greater than 'σu' all results will be unreliable.
Calculated minimum (fully elastic) bending moments (M̂) are exact.
It is expected that the plastic stress calculator is approximately 1% optimistic due to change in shape of the plastic sections of the beam. I.e. the actual bending moments M̌ and M should be between 99% and 100% of the calculated results.
The calculated results will be as accurate as previously described for beams with the entered sectional dimensions. Actual I-Beams and H-Beams are slightly different to the theoretical shapes in the plastic stress calculator (e.g. fillet radii are ignored) and this will be reflected in the accuracy of the result. If you wish to offset this inaccuracy you could alter the flange thickness to generate equivalent cross-sectional areas exactly the same as the actual beam you wish to consider (see CalQlata’s Steel Beams). CalQlata’s assessment of possible variations between actual and entered properties (areas and area moments) of I and H beams should be less than 2%
Further Reading
CalQlata has found little that can be reliably referred to on this subject.
The approach to calculations involving plastic stress and strain described above has been developed by our own engineers

