Flanges (pipeline and piping)
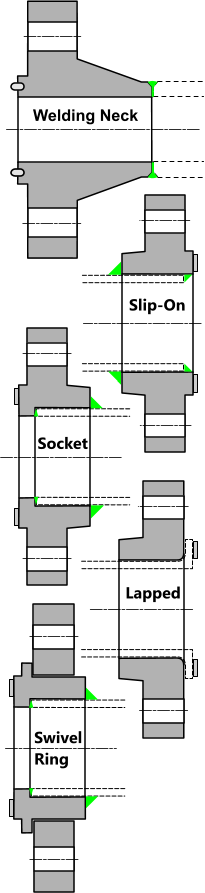
Fig 1. Typical Flange designs
A flange is a means of joining two conduits such as nozzles, pipelines, piping, tubing, etc. that contain flowing and/or pressurised fluid(s). It is usual to ensure that a flanged joint is stronger than the pipe or nozzle to which it is attached, i.e. it is not a focus for weakness, because it would otherwise leak before it fails structurally. Standard flanges are designed to remain pressure-tight even if yield stress is exceeded.
Flange Types
The principle flange designs are show in Fig 1.
Whilst these flanges are, in theory, interchangeable, each type is normally associated with a preferred application.
For example:
Welding Neck (integral) flanges are mostly used in pipelines and for the most demanding applications in terms of mechanical and hydrostatic loading.
Socket (loose) flanges are usually found on small-bore (≤3"), high-pressure, high-flow, multi-phase piping systems where external flange loading is minimal. The socket design provides a smooth-bore through the joint significantly reducing erosion potential from multi-phase fluids.
Slip-On (loose) flanges are for similar applications as the Socket design, except that they are more susceptible to erosion, corrosion, shock loading and vibration. These flanges tend to be used in low-cost, low-demand applications.
Lapped (loose) flanges are for applications where the flange and pipe are not to be welded together. A stub-end is inserted in the flange and the stub-end is butt welded to the pipe. This facility is handy where the flange and pipe are manufactured from different materials. These flanges tend to be reserved for low pressure applications and those where external loads are negligible.
Swivel Ring flanges are used for loose or integral flanges whose bolting ring must rotate to allow for stud-bolt alignment during assembly.
Raised Faces are used for a number of reasons:
1) Easier gasket positioning and visibility
2) Facilitate high pressure (RTJ) gaskets
3) It is easier to install a leak detection facility (Fig 2)
The standard thickness of the raised face is 0.06in (1.5mm) for all flange ratings up to and including 300lb and 0.25in (6.35mm) for all other flange ratings.
The raised face is not included in Flanges' strength calculations. I.e. the length of the flange (L) does not include the raised face thickness.
Gaskets
There are many different gasket designs for flanges but the two most popular are RTJ and 'Spiral Wound'. RTJ gaskets normally comprise soft iron or stainless steel and spiral wound gaskets usually comprise a stainless steel mesh with a suitable filler material.
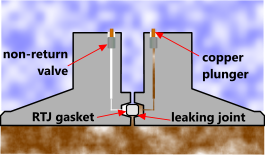
Fig 2. Typical Leak Detection for RTJ
RTJ gaskets are for high-pressure systems and come in a number of designs and materials but they all work similarly in that they seal on the corners of the ring section as opposed to flat gaskets, which seal on their faces. When flanges are installed in areas where inspection is difficult (e.g. subsea) it is useful to install an outwardly visible leak detection facility (Fig 2). A plunger manufactured from copper will ensure it remains free of marine growth.
Flat gaskets are normally used for piping, as opposed to pipeline, systems where the loading conditions are less arduous than typical RTJ applications. Flat gaskets can comprise anything from polymer or vegetable fibre to soft metal (iron, copper, aluminium, etc.). The most common flat gasket is the Spiral wound type.
Refer to CalQlata's Flange Gaskets technical help page for more information on these items.
Design
Gasket size and material will define the bolt loading requirements based either on pressure sealing requirements or external mechanical loading such as bending moments, torsion and/or axial tension.
Flange bolt loading for gasket seating (pressure sealing) and that required for external forces are not added together. Flange bolt loading will constitute the highest requirement, i.e. either that for gasket seating or for external loading, whichever is the greater. It is important to ensure that the gasket material is selected accordingly.
Flange Stresses
A flange is loaded in three ways:
1) Bolting load
2) Internal pressure
3) External forces and moments
As the bolting load must be sufficient to restrain the internal pressure and the external forces and moments, the bolt load will always define the size and strength of the flange.
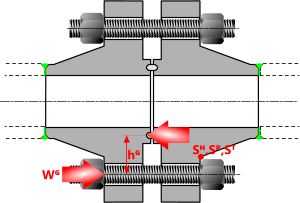
Fig 3. Flange Loads and Stresses
The highest stresses induced in a flange are usually at the intersection between the hub OD and the back of the flange as a result of the bending moment induced between the bolts and the gasket (Fig 3: Mᴳ = Wᴳ x hᴳ).
Because the highest stresses in a bolted flange are highly localised and dissipate over a very short distance, it is acceptable that the calculated longitudinal stress (Sᴴ) is allowed to exceed yield. The tangential (Sᵀ) and radial (Sᴿ) stresses, however, are pressure carrying and therefore limited to yield stress.
Standards
Standard flanges are designed to accommodate standard piping for insertion and/or welding, the most recognised international standard for which is API 5L and the most recognised international standards for flanges are API 605 and ANSI B16-5. The most widely recognised international design (calculation) code for these flanges is ASME VIII. CalQlata's flange calculator is therefore predominantly based upon these design standards/codes.
Design Code
ASME VIII is the most widely known and internationally recognised design code for pipeline flange calculations and ANSI B 16-5 is the most widely known design code for piping systems. As ASME and ANSI are now conjoined, ASME/ANSI has become the most appropriate design code for all pipeline and piping systems. Whilst API also provides a design specification (sizing details) for their pipeline flanges, it is similar to the ANSI design but does not provide a comprehensive calculation facility. Almost all design calculation codes and standards today tend to be based upon the ASME code.
It is for this reason that CalQlata has based its flange calculator on:
ASME VIII, Division 1, Appendices 2, P and S
Flange Cladding
Where flanges are clad with a different material to its main body, e.g. Inconel, Monel, 316, Duplex, etc., the cladding material should not be included in the flange calculations as they will have a different elastic properties to those of the main body of the flange and will therefore react differently to loads imposed on the flange itself.
Flanges Calculator – Technical Help
The Flanges calculator includes a database of flange sizes and a calculation facility to determine their suitability according to the ASME VIII design code.
The input data follows CalQlata's symbology and the output data follows that provided in the ASME VIII design code. The output data is complete according to Sub-Section 2-3 'Notation' of the design code to help you to verify the flange calculator's results. For this reason; where input and output data are for exactly the same property or dimension, their symbols may differ, e.g. whilst the inside diameter of the flange is designated thus 'Øᵢ' in the input data, it is designated thus 'B' in the output data.
The two unit systems accommodated in this calculator are metric (mm and N) and Imperial (ins and lbf).
Calculation Tips
If you are finding it difficult to reduce your stresses to an acceptable level, it is probably because the allowable bolting stress (σᴮ) is too high. The ASME design code assumes you will be applying the allowable bolting stress during assembly. If this proves too arduous for your flange, you could increase its thickness (t), reduce the allowable bolt stress or (slightly) reduce the bolt size. Conversely, if insufficient stresses are applied during installation, the flange could become loose over time due to material relaxation and ultimately leak.
Reducing the seating stress (y) and Gasket factor (m) also helps with reducing flange stresses. For example; try using Monel or Inconel⁽¹⁾ instead of stainless steels such as AISI 304 and 316.
The maximum bolt load (W), which is used for calculating the flange stresses is selected from the highest of the various load cases: 'Wᵐ¹', 'Wᵐ²', 'Wᴼ', 'Wᴳ'. By comparing 'W' with the others, you will see which of them is causing the problem.
For Lapped flanges, see Accuracy below.
Flange Database
The flange database includes the following:
Designs: Lapped, Socket, Slip-On and Welding Neck
Specifications: ANSI, API, BS and MSS
Bore Sizes: ½" to 48"
Pressure Ratings: 150lb to 2500lb
Input Data
Each time a different flange design/size is selected from the database, the following input data is updated automatically:
outside diameter (Øₒ)
butt diameter (Øᵂ)
inside diameter (Øᵢ)#
thickness (t)
length (L)
hub diameter (Øᴴ)
raised face diameter (Øᴿ)
number of bolts (n)
pitch circle diameter (PCD)
bolt-hole diameter (Øᴮᴴ)
# Note: inside diameter (Øᵢ) is not updated for welding neck flanges as this is a variable and not included in the design code.
All other dimensions and properties (as listed below) will remain unchanged as you switch between flange sizes. Therefore you must take care to ensure that you manually update bolting, gasket and piping/nozzle details as required.
Whilst different allowable material stresses are accommodated for ambient and design temperatures (σₐ and σ respectively), ASME normally recommends that carbon steels begin to lose strength above 650°F (340°C) and alloy steels above 100°F (38°C).
Bolting dimensions ...
Major thread diameter (Øₒᴮ)
Minor thread diameter (Øᵢᴮ)
Thread pitch (Pᴮ)
... can be obtained from CalQlata's ThreadsThreads and Threads+ programs.
Gasket dimensions:
Gasket pitch diameter (Øᴳ) is the diameter through the middle
of its manufactured width ('N').
Basic gasket width (bₒ) is the width in direct contact with the flange under full compression. For RTJ gaskets this is normally taken as width ÷ 8⁽²⁾ (ASME VIII, Division 1, Appendix 2, Table 2-5.2)
Both of which will need to be established manually unless you can import them from CalQlata's Flange Gaskets calculator.
The following gasket related input data can be found in;
ASME VIII, Division 1, Appendix 2, Table 2-5.1 or CalQlata's flange gaskets technical help page
Gasket factor (m) ranges from 1.0 for the softest (rubber) materials to 6.5 for stainless steel
Seating stress (y) ranges from 0.2ksi for the softest (rubber) materials to 26ksi for stainless steel
Except for special designs and materials, internal pressure (p) should not exceed the pressures in the following table:
Up to 650°F (340°C), carbon steel flanges should not exceed the pressure for each designated rating between -28 to 38°C
Alloy steels flanges should not exceed the pressure for each designated rating at the listed temperatures
| N/mm² (psi) |
150lb | 300lb | 400lb | 600lb | 900lb | 1500lb | 2500lb |
|---|---|---|---|---|---|---|---|
| -28 to 38°C (-18 to 100°F) |
1.96 (284) |
5.11 (741) |
6.81 (988) |
10.21 (1481) |
15.32 (2222) |
25.53 (3703) |
42.55 (6171) |
| 50°C (122°F) |
1.92 (278) |
5.01 (727) |
6.68 (969) |
10.02 (1453) |
15.02 (2178) |
25.04 (3632) |
41.73 (6052) |
| 100°C (212°F) |
1.77 (257) |
4.64 (673) |
6.18 (896) |
9.28 (1346) |
13.91 (2017) |
23.19 (3363) |
38.65 (5606) |
| 150°C (302°F) |
1.58 (229) |
4.52 (656) |
6.03 (875) |
9.05 (1313) |
13.57 (1968) |
22.61 (3279) |
37.69 (5466) |
| 200°C (392°F) |
1.4 (203) |
4.38 (635) |
5.84 (847) |
8.76 (1271) |
13.15 (1907) |
21.91 (3178) |
36.52 (5297) |
| 250°C (482°F) |
1.21 (175) |
4.17 (605) |
5.56 (806) |
8.34 (1210) |
12.52 (1816) |
20.86 (3025) |
34.77 (5043) |
| 300°C (572°F) |
1.02 (148) |
3.87 (561) |
5.16 (748) |
7.75 (1124) |
11.62 (1685) |
19.37 (2809) |
32.28 (4682) |
| 350°C (662°F) |
0.84 (122) |
3.7 (537) |
4.93 (715) |
7.39 (1072) |
11.09 (1608) |
18.48 (2680) |
30.8 (4467) |
| 375°C (707°F) |
0.74 (107) |
3.65 (529) |
4.86 (705) |
7.29 (1057) |
10.94 (1587) |
18.23 (2644) |
30.39 (4408) |
| 400°C (752°F) |
0.65 (94) |
3.45 (500) |
4.6 (667) |
6.9 (1001) |
10.35 (1501) |
17.25 (2502) |
28.75 (4170) |
| 425°C (797°F) |
0.56 (81) |
2.88 (418) |
3.83 (555) |
5.75 (834) |
8.63 (1252) |
14.38 (2086) |
23.96 (3475) |
| 450°C (842°F) |
0.47 (68) |
2.0 (290) |
2.67 (387) |
4.01 (582) |
6.01 (872) |
10.02 (1453) |
16.69 (2421) |
| 475°C (887°F) |
0.37 (54) |
1.35 (196) |
1.81 (263) |
2.71 (393) |
4.06 (589) |
6.77 (982) |
11.29 (1637) |
| 500°C (932°F) |
0.28 (41) |
0.88 (128) |
1.17 (170) |
1.76 (255) |
2.64 (383) |
4.4 (638) |
7.33 (1063) |
| 525°C (977°F) |
0.19 (28) |
0.52 (75) |
0.69 (100) |
1.04 (151) |
1.55 (225) |
2.59 (376) |
4.32 (627) |
| 540°C (1004°F) |
0.13 (19) |
0.33 (48) |
0.43 (62) |
0.65 (94) |
0.98 (142) |
1.63 (236) |
2.72 (395) |
Special Designs
You can overwrite (modify) any database input value you wish and the calculation will be corrected incorporating your modified value. However, if you change the flange to a different size or type the modified value will be lost.
Slip-On flange calculations can be used for Socket flanges greater than 3" as the calculations are identical and the Slip-On flange database includes sizes up to 48". You simply need to include the inner lip and the raised face in your final design drawings/specification.
Output Data
The output data list and symbology is similar to that shown in ASME VIII, Division 1, Appendix 2, 2-3 Notation.
The calculations for Lapped, Socket and Slip-On flanges are 'loose' in accordance with ASME VIII.
The calculations for Welding Neck flanges are 'integral' in accordance with ASME VIII.
Note the values for 'N' and 'w' (ASME VIII, Division 1, Appendix 2, Table 2-5.2) will automatically be set to zero in this calculator unless gasket information has been imported from CalQlata's Flange Gaskets calculator
A calculation result for a swivel ring that is based upon the same ID as the hub OD (Øᴴ) is provided at the bottom of the output data page. If this stress is too high, you simply increase the flange thickness (t) until it becomes acceptable. If your flange does not have a swivel ring, then ignore this result.
Effective gasket seating width 'b' (ASME VIII, Division 1, Appendix 2, Table 2-5.2) is calculated in the flanges calculator based upon the basic gasket width 'bₒ' that you enter or import from CalQlata's Flange Gaskets calculator.
Imported Data
The flange calculator imports the following data from CalQlata's Flange Gaskets calculator:
'Øᴳ' (gasket pitch diameter)
'bₒ' (basic gasket width)
'N' (gasket width)
'w' (flange nubbin width)
Applicability
These calculations apply to the designs included in the calculator's database, and to any dimensional modifications you make to them.
Flanges only applies to circular flanges of the types shown in Fig 1
Accuracy
The accuracy of these calculations is in accordance with the above mentioned Design Code
However, care should be taken with allowable stresses for Lapped flanges in that they do not provide the same level of support as the Socket and Slip-On designs as the flange is not welded to the pipe. Therefore, CalQlata would recommend that the allowable bolt and flange stresses in Lapped flanges are kept to within 90% of the yield stress for the material concerned.
Notes
- Flange gaskets normally comprise softer grade nickel based alloys allowing you to reduce the variables 'm' and 'y' by about 15%
- Whilst ASME recommends that the effective gasket width (bₒ) is the gasket width divided by 8 for all RTJ gaskets, those manufactured from soft (pure) iron can (and CalQlata believes should) be divided by 6. Moreover, 'w' which ASME uses to define 'bₒ' for RTJ flanges is actually a nubbin width and not a gasket width ('N'). As there is no nubbin in RTJ ring grooves, CalQlata's flange gaskets calculator bases 'bₒ' for RTJ gaskets on 'N' and not on 'w'.
Further Reading
You will find further reading on this subject in reference publications(47, 48 & 49)

