Partial Pressure Calculator
(Dalton's Law)
'Partial pressure' is the term used to describe the pressure of an individual gas within a mixture of fluids. A mixture of fluids means more than one gas and/or a liquid, all of which are equally and evenly dispersed in the same vessel or space. This relationship remains true only for gases that do not chemically react with the other fluids, i.e. at relatively low temperatures.
Gases & Liquids
At the beginning of the 19th century John Dalton discovered that any gas will occupy and fill a space entirely as though no other fluids were present. Even if the volume of the container is such that in order to fill it, the gas would need to settle at a pressure less than ambient, it would do so irrespective of the number of molecules involved. Except for the influence of gravity, the effect of which will be negligible in containers just a few metres high, all gases will always distribute evenly. This phenomenon is known as Dalton's Law.
Whilst all gases and some liquids (e.g. tea and milk) can and will fully occupy their space evenly and equally, some liquids will not; such as oil & water, which do not readily mix and will settle in layers (strata) according to density.
Irrespective of whether or not a container is open or closed, a liquid will always settle to the lowest possible level in it, whilst gases will not. Gases will spread out evenly to fill a closed container or behave as if an open container did not exist.
Saturation
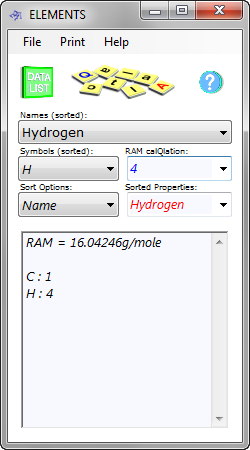
Fig 1. RAM Calculation
Gases cannot become saturated when mixed with other gases
Liquids will become saturated if too much gas is entrained
When entrained in a liquid, all gases will uniformly occupy the same space as the liquid until saturation occurs, at which point gas bubbles will appear and gather together (if contained) or escape (if uncontained) at the top of the liquid. The partial pressure of gas entrained in a liquid will not necessarily be the same as the pressure of the gas at the top of the container.
The Atmosphere
CalQlata has generated a theoretical analysis of all the gases in the earth's atmosphere. It is for systems such as this that partial pressure calculations are most useful. The calculation of partial pressures enables us to define exactly how much of each gas exists at any particular altitude and the altitude of its ceiling. When we say ‘exactly’, we actually mean for a global average, as the weather generates localised variations in pressure and temperature.
In fact this partial pressure calculator has the earth’s atmospheric gases programmed in as its default input values, so you can immediately see the partial pressures of each atmospheric gas. From the pressure of each gas you can identify its density and therefore its column height (see Earth's Atmospheric Gases {the theory}) giving you the actual mass of each gas in the atmosphere.
Testing
E.g. fluid pressure tests such as that described in the API specification 16C for choke and kill equipment where you are required to perform the test using a specific mixture of gases and liquids at high pressure and temperature. In order to ensure that you use the correct quantity (mass) of each gas in your test you must first calculate the partial pressure of each at the the test temperature (see Example Calculation below).
Calculation Process
CalQlata believes that a correct percentage between mixed gases must be based upon mass as opposed to volume, which varies with pressure and temperature.
You calculate the pressure each gas would exert on itself (and the other gases) based upon its mass. You then repeat this exercise for all the other gases in the mixture. Finally you simply add up the pressure of all the gases
Partial Pressure Calculator - Technical Help
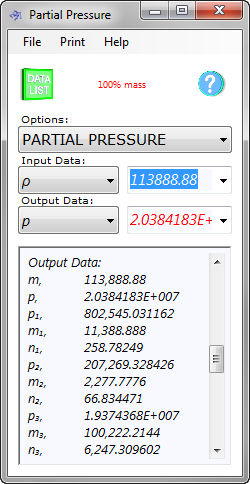
Fig 2. Partial Pressures
Units
You may use any units you like, but you must be consistent.
The Calculation
Partial Pressure asks you for a density (ρ) and a volume (V) of the pressurised mixture, from which the calculator will determine the total mass of the mixture.
You then enter your percentages (%₁ to %₁₂) and relative atomic (or molecular) masses (RAM₁ to RAM₁₂ - CalQlata's Table of the Elements database will calculate these for you: Fig 1) for each substance and the output data will provide you with a total pressure (p). All you do is modify the density (ρ) until you achieve the correct pressure (p).
Example Calculation
Find the partial pressures in a 1m³ container filled with: 90% seawater and 10% gas. The gas is to be a mixture of: 10%:carbon dioxide (CO₂), 2%:hydrogen sulphide (H₂S) and 88%:methane (CH₄) all pressurised to 1.03421368E+008N/m² (15,000psi).
Seawater: density = 1025kg/m³
Total density = 1025 ÷ 90% = 1138.889kg/m³
Gas density = 1138.889 – 1025 = 113.8889kg/m³
Because the following RAM values are in 'g/mole' the total density entered (113.8889kg/m³) should be converted into 113888.9g/m³
CO₂: RAM = 44.0095g/mole, %age mass = 10%
H₂S: RAM = 34.08088g/mole, %age mass = 2%
CH₄: RAM = 16.04246g/mole (Fig 1), %age mass = 88%
The resultant pressure (p) for the gas mixture is 2.038E+07N/m² (2,956.4755psi) so the liquid will be pressurised to;
1.0342E+008 - 2.038E+07 = 8.304E+07N/m² (12,043.52psi)
and each gas will be pressurised as follows (Fig 2):
CO₂: 802,545.03N/m² (116.4psi) {mass = 11,388.9g}
H₂S: 207,269.33N/m² (30.06psi) {mass = 2,277.8g}
CH₄: 19,374,368N/m² (2,810.01psi) {mass = 100,222g}
Applicability
The partial pressure calculator is for percentage mass calculations only. Percentage volumes could be calculated using the ideal gas law and mass output data from the calculator, albeit the percentage volumes you achieve will only be valid for the pressure you use in the ideal law calculation.
Accuracy
The results from the partial pressure calculator are exact and accurate in accordance with the input data you enter.
Further Reading
You will find further reading on this subject in reference publications(3, 12 & 35)

