Bimetallic Strip Calculator (heat-shrink)
Bi-metal (or bimetallic) refers to an assembly of metals with different properties. A bimetallic strip comprises a pair of such metals that, when heated, expand at different rates, causing it to deform.
If the two metals are selected carefully, the deformation can be closely controlled and such a strip may be used as a temperature-sensitive a switch.
References to a 'ring' on this page include any tubular component such as a sleeve, liner or pipe.
Changing the temperature of any metal will result in a change in its dimensions. If the temperature rises the metal will grow and if it falls the volume of the metal will decrease. The relationship between temperature and growth is linear and defined by the metal's coefficient of expansion (linear or volumetric), which is also known as linear and cubic expansivity.

Fig 1. Strip Growth
This relationship can be used to an advantage so long as the operating temperature of thermally affected metal remains low enough to ensure that it doesn't return to its assembly dimension(s). Some useful applications are described below.
Bi-Metal Strip
A bimetallic strip is normally used for relays and alarms where a change in temperature can be used to trigger a switch.
The mechanism is a strip comprising two different metals (a composite) with different coefficients of expansion. Both metals are sweated, pressure-welded, bonded or riveted together along a common surface. When the metals are heated (or cooled) they will attempt to grow at different rates causing them to curve (Fig 1).
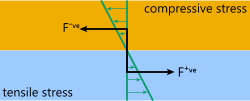
Fig 2. Moment Couple
The forces generating this curve are the equal and opposite axial reaction forces ('F' Fig 2) in the metals generated by their stresses (one compressive and the other tensile) due to their differing rates of expansion, which in turn generates a moment couple causing it to bend. The bend radius will only be smooth and consistent if the bonding between the two metals is equally strong throughout the joint.
Heat-Shrink Ring Calculations
A heat-shrink ring or sleeve can be used where it is needed for protection from problems such as corrosion, wear or impact but may need regular replacement. This ring (or sleeve) can be removed either by machining it off again or re-heating it. Re-heating it for removal will only work, of course, if the core can be prevented from reaching the same temperature.

Fig 3. Heat Shrinking
Should you wish to use the ring to drive another component (such as a gear or spline) it would be advantageous to machine keyways in the mating surfaces.
Heat shrinking is the process of allowing a heated ring to cool when assembled onto a circular core (Fig 3). You simply machine the inside diameter of the ring slightly smaller than outside diameter of the core. To assemble the two (ring and core) you then heat up the ring to a temperature that will expand the internal diameter greater than the core's outside diameter, slide it over the core and let it cool down. The resultant grip and hoop stress in the ring will be as a direct consequence of the difference between the ring ID and the core OD when cold (or at operating temperature). The greater the difference, the higher the grip but also the higher the stresses in both the ring and the core. The trick is to optimise stress and grip to accommodate the operating temperature for the assembly.
Freeze-Grow Ring Calculations
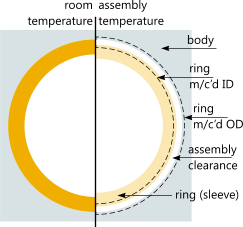
Fig 4. Freeze Growth
Just as with heat-shrink components, a freeze-grow ring can be used where it is needed for protection from problems such as corrosion, wear or impact but may need regular replacement. This ring can be removed either by machining it off again or re-cooling it. Re-cooling it for removal will only work, of course, if the bored body can be prevented from reaching the same temperature.
Should you wish to prevent the ring from rotating (such as for engine cylinder bores) it would be advantageous to machine keyways in the mating surfaces.
This is the process of allowing a ring to grow into a circular bore whilst returning to room (or operating) temperature (Fig 4). You simply machine the outside diameter of the ring slightly larger than the bore diameter and then cool it sufficiently for it to contract to a diameter smaller than the bore, slide it in and allow it to warm-up naturally. The resultant grip and hoop stress in the ring will be as a direct consequence of the difference between the outside diameter of the ring and inside diameter of the bore. The greater the difference, the greater the grip but also the higher the stresses in both the ring and the bore. As with the heat-shrink ring, the trick is to optimise stress and grip to accommodate the operating temperature for the assembly.
Bimetallic Strip Calculator - Technical Help
Units
You may use any units you like, but you must be consistent.
Bimetallic Strip Calculations
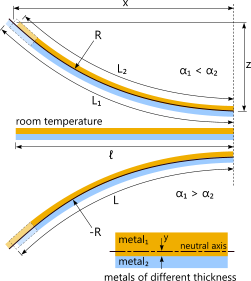
Fig 5. Bi-Metal Bending
The two metals are identified as 'Metal₁' and 'Metal₂'. You may enter the properties for either in any order and the calculation will be equally valid, however, if the radius ('R') is positive the curve in the composite will bend towards Metal₁, i.e. Metal₂ will be on the outside of the bend. Otherwise (i.e. the radius 'R' is negative) the curve will bend towards Metal₂ and Metal₁ will be on the outside of the bend. This radius 'R' is provided at the neutral axis of the composite thickness not necessarily the join between the two metal strips.
Combined growth ('L') is the actual (constrained) expansion as a result of compression and tension between the two metals.
Free growth ('L₁' and 'L₂') is the expansion you would expect if the metal concerned was free to expand without constraint (from the other metal).
A negative output stress ('σ') will mean that the metal concerned will be in axial compression. A positive output stress ('σ') will mean that the metal concerned will be in axial tension.
The force ('F') is axial and the same magnitude in both metals, albeit, 'one of them will always be negative (Fig 2; F⁻ᵛᵉ) and the other will always be positive (Fig 2; F⁺ᵛᵉ)'.
Heat Shrink
Only the ring is considered in this calculation because the calculator has no idea of the shape of the inner core. As such, you will need to apply your grip pressure ('p') as an external pressure or radial stress for your own compression calculations on your core.
The difference between the internal diameter that you enter (Øᵢ) and the machining diameter calculated (Øᴹ) provides the grip pressure (p) you require for assembly.
When selecting your materials and calculating the optimum grip pressure and heating temperature for this type of assembly, you must consider the following:
1) That the heating temperature is well below the melting (or softening) temperature of the metal concerned
2) That the grip pressure is sufficient to prevent slipping at operating temperature and with operating drive loads
3) That the resultant hoop stress ('σ') is well within the limits of the material. It should be remembered that if you set the assembled stress too close to the material's minimum yield and subsequently expose the material to elevated temperatures during operating conditions, the material can relax (self-anneal), reducing its grip
4) That the grip pressure is well within the capability of the core
5) That the two materials are compatible with respect to galvanic corrosion if they are to be placed in an electrolyte
The assembly clearance ('c') is required to ensure you can assemble the ring. Some material may not be perfectly homogeneous and may not deform uniformly during heating, which could make assembly difficult.
Whilst you may enter different material thicknesses and widths for both the metals in the strip, if the widths are sufficiently different the force distribution will become complex and the results may be inaccurate.
Freeze-Grow
All the considerations raised in Heat-Shrink above apply to this procedure with one additional proviso:
When compressing a ring into a bore, just as with external pressure on the wall of a pressure vessel, the ring will deform elastically long before yield stress is reached in the material. Therefore, it is advantageous to ensure that the wall thickness is at least 1/20th of the outside diameter and that hoop stress in the ring does not exceed 40% yield at either operating temperature or room temperature.
Accuracy
The calculations in the bimetallic strip calculator are exact assuming all conditions are perfect and all materials are homogeneous.
Ring thickness variations are included in the calculations for 'heat-shrink' and 'cool-grow' processes.
Further Reading
You will find further reading on this subject in reference publications(2)

