Centrifugal Force Calculator
(rotational velocity and acceleration)
Centrifugal Force
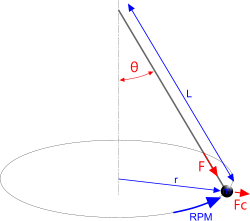
Fig 1. Centrifugal Force on a Mass
Any rotating body is subjected to a centrifugal force (Fig 1 'Fc') that is trying to pull it away from its centre of rotation. In fact every particle (atom, molecule, sub-atomic particle, etc.) in the body is subjected to this force. If a centrifugal force is too high for a body’s internal holding force to withstand, the body will deform or shatter and fly apart (see Wheels below).
This force enables an orbiting body to oppose the gravitational force that would otherwise cause it to fall back towards its holding mass (e.g. planet or star). If the centrifugal acceleration is equal to the gravitational acceleration the rotating body will continue to orbit at the same altitude for ever until conditions change (Fig 2).
Centripetal Force
A centripetal force is the opposing force that tries to pull the body back towards the centre of rotation. It is this force (centripetal) that causes planets to orbit a sun and moons (satellites) to orbit their planets.
For example, a mass attached to the end of a cord or rod that is swung around in a circle has two equal and opposite forces acting on it:
1) A centrifugal force imposed by the body trying to force it away from its centre of rotation
and;
2) A centripetal force in the cord (or rod) pulling it towards the centre of rotation
Satellites
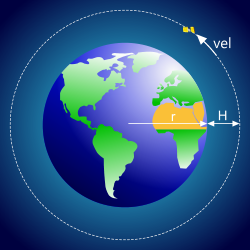
Fig 2. 'Moving' Satellites
Satellites use this natural phenomenon to hold a constant position over the earth. The satellite is released into space at the escape altitude and a velocity sufficient to hold position over the earth’s surface. No altitude correction is required because gravitational acceleration at this altitude is equal to the centrifugal force pulling the satellite back towards the planet. In theory, the only energy required to maintain positional orbit is that which may come from velocity decay and given that the earth has no atmosphere at this altitude (see Earth's Atmosphere) there is nothing to slow the satellite down other than interplanetary gravitational attraction.
If the satellite operates at a lower altitude than the escape altitude, its velocity must be increased in order to achieve a greater centrifugal acceleration to equal the higher gravitational acceleration of the planet at the lower altitude. Because the absolute ceiling of the earth’s atmosphere is 8103.50773km) it would be wise to ensure that your satellite is released above this altitude so that its orbital trajectory doesn’t need to fight against atmospheric resistance.
Wheels
The centrifugal force in a wheel can destroy it if rotation is sufficiently fast. If the mass outside any given radius is sufficient to impose a stress on the cross-sectional area of the wheel at the radius concerned that is greater than the SMYS of the wheel material the wheel will deform. If it is higher than the UTS of the wheel material, the wheel will shatter and fly apart.
Pendulums
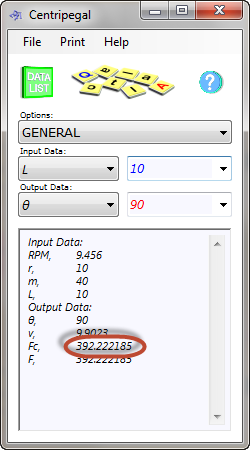
Fig 3. Centrifugal Force on a Body
There has been a good deal of controversy over perpetual motion for centuries. Yet in theory it is possible in a vacuum with no gravitation attraction, but it cannot involve any change of direction. The problem on earth is that after you initiate, for example; a pendulum (linear or circular), ignoring pivot resistance, there are two principal forces trying to slow it down:
1) Drag and added mass resistance from the gases in the air (atmosphere) (see the technical help page for the Added Mass & Drag calculator)
and;
2) Gravitational attraction
To overcome the first problem you could swing the pendulum in a vacuum. Whilst there will be a significant reduction in Amplitude decay, each time the pendulum reaches an inclination equal and opposite to the initiation inclination the earth’s gravity will cause it to return to vertical. Gravity is continually trying to force the pendulum to achieve the lowest energy condition; i.e. point towards the centre of gravitational pull.
You can take the pendulum to outer-space far away from any gravitational influence and swing it again. However, it will no longer act as a pendulum. It will simply rotate, continually. But even this condition will eventually stop the rotation because the centripetal force on the pivot is continually dissipating energy through friction.
For example; the orbit of earth’s moon is considered by many to be perpetual, but it isn’t. It is gradually moving away from the earth by about 2.5cm every year. It will eventually fly away leaving the earth with no tilt stability or tides.
So the only theoretical solution to perpetual motion with no need for energy top-up is to eject it in space in a straight line and hope it doesn’t hit anything or come under gravitational influence from another body.
Centrifugal Force Calculator - Technical Help
Units
You may use any units you like, but you must be consistent.
General
This calculation option covers any rotating mass.
For example; it applies to circus rides where a chair is suspend from a pivoting arm. If a 40kg child is swung around on the end of a 10m long arm at 9.456 revolutions per minute such that the arm is horizontal ('r' and 'L' are equal), the centrifugal force would be about 392N, which is equivalent to the same child standing on the earth’s surface at sea level (i.e. 392/g; Fig 3).
Escape Altitude

Fig 4. 'Static' Satellites
Escape altitude is the tem used by CalQlata to describe the altitude at which an orbiting body or satellite can remain over exactly the same spot ('static' satellite) and because the centrifugal force acting on the body is exactly the same as the gravitational attraction applied to the body by the planet (Fig 4).
If the body orbits at a higher altitude whilst remaining over the same spot, its velocity would increase, raising its centrifugal acceleration but reducing gravitational attraction. Therefore it would gradually fly off into space.
If the body orbited below this altitude at the same velocity or at a lower velocity at this altitude, it would gradually fall back towards the planet.
This altitude for the earth is 35840090.461855m above sea level.
You can calculate the escape altitude for a satellite orbiting faster or slower that the earth’s rotation by modifying the 'RPD' value. For example; if you want to calculate the escape altitude for a satellite orbiting the earth twice every day, you set 'RPD' equal to 2
Whilst this calculation option is designed for the earth it can be used for any planet by modifying the 'RPD' value. I.e. if your planet rotates twice as fast as the earth you must set 'RPD' to 2 for a satellite to remain over the same location. If you want your satellite to rotate around this planet at a different speed, however, you must multiply it again by the orbit factor. For example: if your planet rotates 1.35 times as fast as the earth and you want your satellite to orbit the planet twice for each planetary rotation, you must set the 'RPD' value to 2.7 (RPD = 1.35 * 2)
The details of some other celestial bodies for you to try are provided below:
Mercury: mass ('m₁') = 3.285E+23 kg {7.2422E+23 lbs} and radius ('r') = 24395E+06 m {8.0036E+06 ft}
Jupiter: mass ('m₁') = 1.8981310E+27 kg {4.1847E+27 lbs} and radius ('r') = 6.9911E+07 m {2.2937E+08 ft}
Sun: mass ('m₁') = 1.98910E+30 kg {4.3852E+30 lbs} and radius ('r') = 6.95842E+08 m {2.2830E+09 ft} ⁽¹⁾
Escape Velocity
In this calculation option you can find the altitude required for a body orbiting at a particular velocity ('moving' satellite) or the velocity necessary to maintain a specific altitude. It should be remembered that these calculations assume your satellite is not orbiting in an atmosphere so it should be more than 8103.50773km above the earth's surface (see Satellites above) or the upper atmospheric ceiling for any other planet you consider.
These calculations do not apply only to satellites, of course. In the correct conditions a body can orbit any larger body in outer space, where there is no atmospheric drag. And the Centrifugal calculator can be used to analyse this behaviour. The gravitational constants remain valid for any and all such calculations.⁽¹⁾
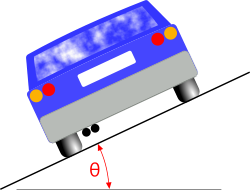
Fig 5. Road Banking for Vehicles
Banking
Whilst this calculation option can be used to calculate the banking angle ('θ') of a conventional road, it can also be used to determine the nominal speed and inclination for ‘wall-of-death’ riding. These are near vertical circular walls inside which people ride cars and motorbikes around at high speed.
For example, a driver (or rider) would need to travel at 50m/s (111.85 miles per hour) around the inside of a wall 100 metres diameter inclined at 78.9° if he/she was to remain at a constant height. Reduce this diameter to 20m and the wall would need to be inclined at nearly 88° for the same speed.
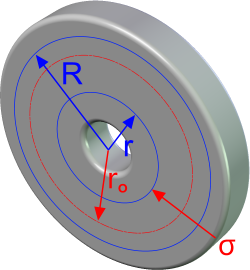
Fig 6. Centrifugal Force on a Wheel
Discs & Wheels
If R = outside radius and r = inside radius of a section of a wheel, the radius of gyration ('rₒ') of the mass between these two radii will define its limiting velocity (Fig 6).
For example; the wheel of a vehicle travelling at 1500km/hr (1500000m/hr) will rotate at; 1500000 ÷ 2.π.R/60 (7957.747 rpm) revolutions per minute ('RPM'). You can use this (or any other) rotational velocity to establish the centrifugal stress in the wheel material.
Enter the speed ('RPM') of your wheel into the centrifugal calculator and it will calculate the stress at the inner radius ('r'), which is where the maximum stress due to centrifugal force will always occur.
If the centrifugal stress ('σ') is close to or greater than the SMYS of the wheel material, it will deform at this speed. If the stress is close to or greater than the UTS of the wheel material, it will shatter at this speed.
Notes
- The centrifugal calculator’s own technical help menu provides metric and imperial values for the gravitational constant ('G') used in this calculation option.
Further Reading
You will find further reading on this subject in reference publications(3)

