Screw Thread Calculator
(strength, capacity & dimensions)
M-Type Screw Threads
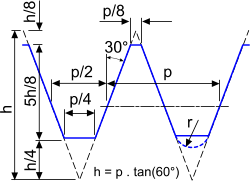
Fig 1. M-Type Screw Thread
Almost all today's primary M-Type helical screw threads (metric, Unified, British, etc.) follow Sir Joseph Whitworth's original mid-19th Century design with minor variations regarding relative dimensions, clearances, tolerances and root radii (see Fig 1 and Threads+ technical help page).
Taper-Lock
Screw threads are a clever bit of engineering. If you straighten one out you will find that it is a simple taper varying between about 4° (smallest screws) to about 2° (larger screws). It is no coincidence that Stephen Morse's 'self-holding' taper has an included angle of about 3°. It turns out that 3° is the optimum slope for two clean, well-machined faces of carbon steel to provide a mechanical lock and yet still part without much effort and no resultant damage.
Optimisation
Furthermore, the diameters and pitches in standard (non-specialised) screws are optimised to ensure that the thread and bolt have equal axial (with respect to the bolt or screw) strength. This design aspect only works if the manufacturing materials are of consistent quality and if the threads themselves have been accurately forged (not machined) into the screw and properly lubricated during assembly.
Lubrication
In order to retain maximum tensile capacity in a bolt, you must induce negligible torsion during tightening. As such, Threads assumes the mating threads are fully lubricated before assembly. Suitable lubrication will normally result in a friction coefficient between 0.1 and 0.3 dependent upon the lubricant used and the materials from which the threads are manufactured. The higher the torque the higher the frictional resistance (as lubricant is squeezed out).
Torsion
Where bolt integrity is vital (e.g. pipeline flanges) bolt-tensioning equipment is normally used, eliminating torsion. For such equipment the 'Max Tension' result (Fmax) should be used as the basis for pre-tensioning loads. Up to 90% of maximum tension may be applied to high-security component assemblies such as pipeline flanges and engine cylinder heads.
Screw Thread Strength
Metric (strength)
- Designations: 3.6, 4.8, 5.8, 6.8, 8.8, 9.8, 10.9, 12.9.
- The first number in the Designation represents the Nominal Tensile Strength (st) of the bolt material (Mpa x 100).
- The second number in the Designation represents its 'Proof Stress (sp) / Tensile Strength (st)' (% x 10).
- e.g. Designation 8.8: st = 800MPa & sp/st = 80%.
Imperial (ANSI/ASME VIII) (strength)
- Designations (low alloy steels): B5 (80,000psi), B7 (≤2½ins:105,000psi & ≤4ins:95,000psi & ≤7ins:75,000psi)
- Designations (high alloy steels): B6 (85,000psi), B8 (30,000psi)
- Designations (Nickel alloy steels): B (≤¾in:115,000psi & ≤3½ins:110,000psi)
Screw Thread Classes of Fit
A brief overview of the most popular classes of fit for metric and imperial threads is given below.
See CalQlata's Threads+.
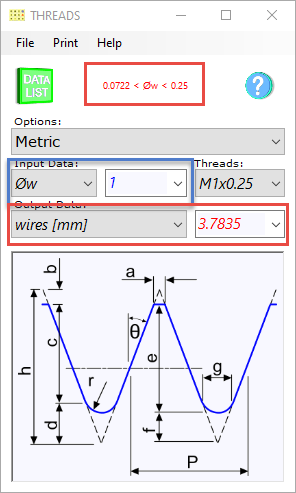
Fig 2. Thread Measurement Using Wires
Metric (class)
- External (bolts); Close fit = 4g, Medium fit = 6g, Free fit = 8g
- Internal (nuts); Close fit = 5H, Medium fit = 6H, Free fit = 7H
Imperial (class)
- External (bolts); Close fit = 3A, Medium fit = 2A, Free fit = 1A
- Internal (nuts); Close fit = 3B, Medium fit = 2B, Free fit = 1B
Screw Thread Strength Calculator - Technical Help
When calculating the tensile capacity of a threaded screw (see the note at the bottom of this page) and the associated torque required to achieve it, you will be asked to enter the specified minimum yield strength (SMYS) of the material and the coefficient of friction between the internal and external threads. You must enter your SMYS value in metric [N/mm²] or imperial [psi] according to the thread type you select) and as you switch between metric and imperial threads, the calculator will automatically convert the strength for you.
However, unless the material and manufacturing methods are well known, care should be taken in selecting reliable SMYS values, e.g. >50% of the expected strength is rarely achievable from machined screw threads.
Note:
Bolt strength as calculated in Threads is a close approximation for the strength of the shaft of the bolt. For a much more accurate assessment of thread assembly strength you should use the Threads+.
Thread Measurement
The threads calculator includes a measurement facility using wires. If you enter a suitable wire diameter (Øw), Threads will provide the expected measurement (wires) across them.
You will be warned if the wire size entered is unsuitable (Fig 2)
Further Reading
You will find further reading on this subject in reference publications(2 & 3)

