Planetary Spin Calculator
This web page and the maths associated with this calculator are copyright protected by
Keith Dixon-Roche {© 14/03/17}
Terminology
1) Gravitational energy is the same as potential energy. As this web page deals with Newtonian mechanics only the term gravitational energy will be deployed.
2) Suffixes apply as follows:
'ₒ' = satellite orbit; '₁' = force-centre; '₂' = satellite; '₃' = secondary satellite
3) Refer to our Planetary Spin web page on for a detailed breakdown of the maths used in this calculator
Planetary System (Fig 1)
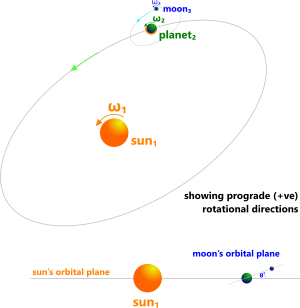
Fig 1. Planetary System
Planetary spin refers to the angular rotation (spin-rate) induced in a celestial satellite in orbit around a force-centre, such as a star or planet.
The body being investigated is a satellite
(e.g. as sun, planet or moon)
Its force-centre is a galactic star, solar sun or planet
Its secondary satellite(s) is a planet or moon
What Is Planetary Spin?
It is the spin rate of a force-centre or satellite. It has both [angular] velocity and direction.
Whilst it is not part of Newtonian mechanics, the energy that generates spin is found in Isaac Newton's laws of motion.
What Are Spin Energies?
Spin energy is the rotational energy inducing spin in a satellite.
Orbital Energy (Eₒ)
Assuming no other [energy] influences, gravitational energy will ensure that a satellite orbiting a force-centre will always present the same face to its force-centre causing it to spin at an angular velocity (ωₒ) with the same period as its orbital period
Force-Centre Energy (E₁)
This is the rotational energy induced in a satellite due to its own orbital kinetic energy, which varies with its distance from its force-centre according to Isaac Newton's inverse-square relationship. This energy will cause a satellite to rotate in the opposite direction to ωₒ
This energy can be found in Newton's output data for the satellite
Force-Centre Energy (E₃)
This is the rotational energy induced in a satellite by its own secondary satellites and will cause a satellite to rotate in the same direction as the secondary satellite's orbit. Its magnitude is dependent upon the relative angle between the satellite's orbital plane and that of its secondary satellites.
This energy can be found from the [sum of] Newton's output data for the orbit of each of the secondary satellite(s)
Moons or No Moons!
Apart from Mars, all the planets in our solar system possess spin energy from secondary satellite(s) at least a thousand times greater than that induced by the satellite's own kinetic energy. This is why Venus rotates in the opposite direction to the other planets; it has no secondary satellites to overcome the influence of E₁
Mars is a very special case because it appears to be hollow. The influence of its secondary satellites is only 2.5 times greater than E₁. Phobos actually rotates faster than its force-centre (Mars), which must be due to Mars' unusually low 'Δ' value
Example Calculation 1
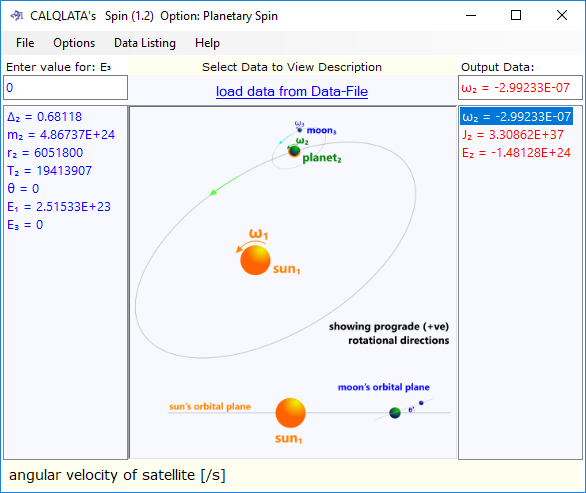
Mercury & Venus have no moons, so we shall calculate the spin in both planets (Fig 2 shows the calculation for Venus)
| Property | units | Mercury | Venus |
|---|---|---|---|
| Newton Calculation | |||
| m₁ | kg | 1.9885E+30 | 1.9885E+30 |
| m₂ | kg | 3.30110E+23 | 4.86737E+24 |
| r₂ | m | 2439700 | 6051800 |
| T₂ | s | 7600522 | 19413907 |
| R̂ | m | 4.60012E+10 | 1.07477E+11 |
| E₁⁽¹⁾ | J | 5.76563E+23 | 2.51533E+23 |
| Spin Calculation | |||
| m₂ | kg | 3.30110E+23 | 4.86737E+24 |
| r₂ | m | 2439700 | 6051800 |
| Δ₂ | 0.812863 | 0.68118 | |
| T₂ | s | 7600522 | 19413907 |
| θ | ° | 0 (no moons) | 0 (no moons) |
| E₁ | J | 5.76563E+23 | 2.51533E+23 |
| E₃ | J | 0 (no moons) | 0 (no moons) |
| J₂ | kg.m² | 5.19309E+35 | 3.3086276E+37 |
| E₂ | J | 3.99116E+23 | -1.48128E+24 |
| ω₂ | ᶜ/s | 1.2398E-06 | -2.99233E-07 |
| Planetary spin in planets with no moons 1) output data from Newton for the satellites (Mercury and Venus) |
|||
Example Calculation 2
Neptune is a little more complicated as it has many moons, three of which orbit in the opposite direction (retrograde) to Neptune's own orbit (prograde)
| Neptune's Moon | E₃ (J) |
|---|---|
| Naiad | -1.41526E+25 |
| Thalassa | -2.72711E+25 |
| Despina | -1.30039E+26 |
| Galatea | -2.20708E+26 |
| Larissa | -2.30921E+26 |
| S/2004 N 1 | -1.63551E+23 |
| Proteus | -1.44926E+27 |
| Triton | -2.05897E+29 x -1 |
| Nereid | 1.12539E+26 |
| Halimede | 2.56883E+21 |
| Laomedeia | 1.15675E+22 |
| Sao | 4.34646E+21 |
| Neso | 1.84075E+22 x -1 |
| Psamathe | 1.80844E+21 x -1 |
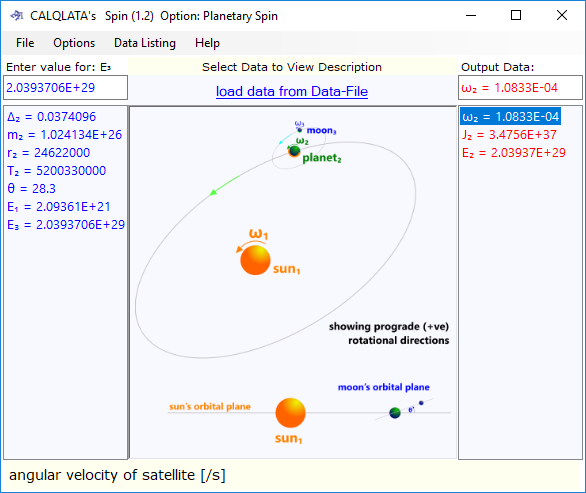
| ΣE₃ | 2.0393706E+29 # |
| Planetary spin energies calculated using the Newton calculator | |
| Property | units | Neptune | |
|---|---|---|---|
| Newton Calculation | |||
| m₁ | kg | 1.9885E+30 | |
| m₂ | kg | 1.024134E+26 | |
| r₂ | m | 24622000 | |
| T₂ | s | 5200329600 | |
| R̂ | m | 4444450000000 | |
| E₁⁽¹⁾ | J | 2.09361E+21 | |
| Spin Calculation | |||
| m₂ | kg | 1.0241340E+26 | |
| r₂ | m | 24622000 | |
| Δ₂ | 0.0374096 | ||
| T₂ | s | 5200329600 | |
| θ | ° | 23.8 | |
| E₁ | J | 2.09361E+21 | |
| E₃ | J | 2.039371E+29 # | |
| J₂ | kg.m² | 3.4756E+37 | |
| E₂ | J | 2.03937E+29 | |
| ω₂ | ᶜ/s | 1.0833E-04 | |
| Planetary spin in the planet Neptune 1) output data from Newton for the satellite (Neptune) |
|||
Delta Value (Δ)
The delta value of any satellite or force-centre is the factor that must be applied to its radius in order to accurately define its polar moment of intertia, which can be used to define its structure using Core Pressure theory
Planetary Spin Calculator - Technical Help
Units
You may use any units you like, but you must be consistent.
Input Data
The two available calculation options allow you to input either:
Δ₂: the delta value of the satellite to calculate its angular velocity (ω₂)
or
ω₂: the angular velocity of the satellite to calculate its delta value (Δ₂)
m₂: mass of the satellite
r₂: volumetric radius of the satellite
T₂: orbital period of the satellite [seconds]
θ: angle between the orbital plane of the satellite and that of its secondary satellites [degrees]
E₁: the energy induced into the satellite by its force-centre. This value may be obtained from CalQlata's Newton calculator from a calculation of the satellite itself
E₃: the total (ΣE₃) energy induced into the satellite by all of its secondary satellites. This value may be obtained by summing-up the individual E₃ energy values for each of the secondary satellites, which can be found using Newton
Output Data
ω₂: the angular velocity of the satellite; if the satellite's delta value (Δ₂) was entered
or
Δ₂: the delta value of the satellite; if the satellite's angular velocity (ω₂) was entered
J₂: polar moment of inertia of the satellite
E₂: total spin energy generating ω₂
Applicability
This calculator can be used for any satellite orbiting a force-centre
Accuracy
This calculator is as accurate as Newton's own laws of motion
Further Reading
You will find further reading on this subject in reference publications(55, 61, 62 & 64)

