Newton's Laws of Orbital Motion Calculator
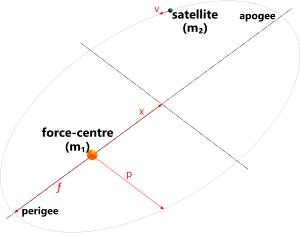
Fig 1. Orbital System
In this and other pages associated with the Newton calculator, the term satellite refers to any natural mass (m₂) such as a planet or moon, freely orbiting a force-centre (m₁) such as a star or planet in a vacuum.
The Orbital System
A typical orbital system is shown in Fig 1. The orbital perigee is the point at which the satellite is closest to the force-centre and the orbital apogee is the point at which the two are farthest apart. These two points are at opposite ends of the major axis of the orbital ellipse.
Laws of Orbital Motion
A detailed description and explanation for all the formulas used in this calculator can be found on our web-page: Laws of Motion, most important of which is that 'evergy orbital system must include a force-centre and at least one satellite'. This is how we know that our Milky Way galaxy has its own force-centre
Newton developed his laws without the knowledge of spin theory, which is understandable given that it wasn't known in the 17th century exactly how much spin existed in the sun or its orbiting planets. Spin theory defines the laws governing the spin (rotation) in force-centres and their orbiting bodies. This theory remained unsolved until 2017 but can now be found on our web-page; Planetary Spin
It was the omission of spin theory, together with a misunderstanding of Newton's fundamental laws of orbital motion (see above) that two early 20ᵗʰ century scientists (Fritz Zwicky & Jacobus Kapteyn) invented dark matter to keep galaxies together. In reality, dark matter is not necessary (as can be proven by this calculator) and therefore does not exist. The properties of our Milky-Way's force-centre are now known.
I.e.:
NASA suggests that our sun is 1E+21 metres from the centre of the galaxy and that it will take 230 million years to orbit the Milky Way, and Wikipedia suggests that the galaxy contains 250 billion ± 150 billion stars
Using this information, along with the sun's known properties, we can now calculate the sun's orbit in the Milky Way using Newton's laws of motion thus:
m₁ = 1.76572018982348E+41 kg
m₂ = 1.9885E+30 kg
Tₒ = 7.258248E+15 s
R̂ = 2.4653729E+20 m
G = 6.67359232004332E-11 m³/s²/kg
i.e. the Milky Way's force centre is 1.76572E+41 kg (rotating at 6.364E-8 radians per second)
The calculation will be equally applicable even if NASA and Wikipedia are incorrect, albeit the force-centre mass and angular speed will vary slightly. According to the Newton's gravitational force, the average density of Hades maust be similar to that of iron than that of a neutron star as its core pressure is insufficient to generate fusion through gravity alone.
Newton's laws of motion apply to all force-centres with orbiting bodies, including atoms. Therefore, this calculator may be used to calculate the performance of electrons in atoms as long as the coupling ratio is applied to the orbital; energies, forces, velocities and accelerations, because electrical (not gravitational) forces are holding the atom together.
Newton's laws also show that any satellite (star, planet, moon, etc.) can be extracted from its own orbit and slotted into any other. Try inserting Jupiter in earth's orbit using this calculator, it works!
Newton's Gravitational Constant (G)
Newton never specified his gravitational constant (G) when he published his Principia, which is understandable because no doubt he did not realise that it is actually based upon elementary particles. This constant has continued to be the subject of estimation; until now.
'G' has now been solved and can be found on our web-page; 'Newton's 'G'' and its correct value is defaulted in the Newton calculator. Hence you will notice the difference between the 'units of convenience' (N.kg²/m²) that have been applied to this constant to date and its actual units (m³ / kg.s²) as provided in the calculator.
Newton's Laws of Orbital Motion – Technical Help
Units
You may use any units you like, but you must be consistent.
Refer to Input Data and Output Data below for examples of the {units} you get out from those you enter. The {units} provided below are those for the defaulted data.
Units in [square brackets] are fixed; i.e. they cannot be altered
Alternative Input/Output Data
m₁ = the mass of the force-centre {kg}
Rᴬ = the radial distance between the centres of mass of the force-centre and the satellite at its orbital apogee {m}
K = the constant of proportionality {s²/m³}
Common Input Data
m₂ = the mass of the satellite {kg}
Rᴾ = the radial distance between the centres of mass of the force-centre and the satellite at its orbital perigee {m}
t₂ = the period the satellite takes to complete its orbit [seconds]
θ = the angle through the orbital path from the orbital apogee [°]
G = Newton's gravitational constant which is provided in the Newton calculator in m³/s²/kg, you will need to convert this value into your preferred units if different
(e.g. 1.19176793676718E-09 in³/lb/s²).
Common Output Data
Orbital Shape
R = the radial distance between the centres of mass of the force-centre and the satellite at θ {m}
a = the major semi-axis of the elliptical orbit {m}
b = the minor semi-axis of the elliptical orbit {m}
e = the eccentricity of elliptical orbit (0 ≤ e < 1) {0 means the orbit is circular}
½p = the orbital [half] parameter
ƒ = the radial distance between the centres of mass of the force-centre and the satellite at the satellite's perigee {m}
x = the radial distance between the centre of mass of the force-centre and the geometric centre of the ellipse {m}
L = the total length (circumference) of a single orbit {m}
A = the total area enclosed by orbital ellipse {m²}
v = the satellite's orbital velocity at θ {m/s}
g = the gravitational acceleration exerted by the force-centre on the satellite at θ {m/s²}
a = the centrifugal acceleration on the satellite at θ {m/s²}
Fg = the gravitational force between the force-centre and the satellite at θ {N}
Fc = the centrifugal force in the satellite at θ {N}
PE = the potential (gravitational) energy in the satellite at θ {J}
KE = the kinetic energy in the satellite at θ {J}
E = the total energy in the system (satellite and force-centre), which remains constant throughout the orbit {J}
Applicability
The Newton calculator can be used for any force-centre/satellite system in which gravity is the sole coupling force.
Accuracy
The calculations in the Newton calculator are as accurate as the input data used.
You will notice some variation between 'g' and 'a' (and therefore 'Fg' and 'Fa'). This is due to inaccuracies in the orbital data (planetary and star masses and orbital radii) that have been taken from various sources.
Orbital energies (PE and KE) are based upon gravitational acceleration (g).
The total energy (E) should be identical all around the orbit (conservation of energy).
You will find that this is not the case according to the input data provided for each planet in the technical help page that comes with this calculator, which has been taken from NASA's planetary fact-sheets. The problem will be the perigee radial distances (Rᴾ) all of which are slightly incorrect.
You can play with these input values (Rᴾ) until conservation is achieved should you wish. NASA's [incorrect] values have been provided simply for reasons of verifiability.
Further Reading
You will find further reading on this subject in reference publications(61, 62, 63 & 65)

