Optical Lens Calculator
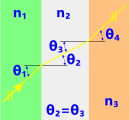
Fig 1. Parallel Faces
A lens is a device that magnifies or shrinks a source of EME radiation.
The lenses with which we are most familiar are the optical (light) type and constitute the subject matter of this page.
Important Note: 'light velocity' (v) on this page refers to the time taken (t) for EME to pass through the thickness (d) of the medium concerned; v = d ÷ t.
In reality, EME velocity is a constant, irrespective of the medium through which is is travelling; it never changes; this velocity is 'c'.
The reason EME velocity appears to slow down when travelling through a medium, is because it gets diverted as it tries to pass between adjacent atoms and/or molecules. And generally, the greater the medium density, the longer the EME will take to traverse it. In other words; the greater the molecular (or atomic) intensity, the longer it will take to get through.
In this instance, 'intensity' refers to the EME amplitude relative to the inter-atomic distances in the medium. I.e. the smaller the EME amplitude relative to the intensity, the less the EME will be deviated from its path and the quicker it will pass through the medium.
Refractive Index (n)
Light travels at 'c' velocity through a vacuum and 'n' times slower than 'c' through any and all other media. For example:
nair = 1.000308502
nfresh water = 1.33333
ndiamond = 2.41768
i.e. light travels through air at a speed of; c ÷ 1.000308502, and is also its refractive index. Therefore the refractive index of any medium is the ratio of the speed of light in a vacuum and the speed of light in that medium.
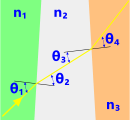
Fig 2. Diverging Faces
Snell's law is the relationship between the angles of incidence⁽¹⁾ of light travelling through adjacent media of differing refractive indices, which he described as follows:
n₁.Sin(θ₁) = n₂.Sin(θ₂) = n₃.Sin(θ₃) = n₄.Sin(θ₄) = ...
where 'θ' is the angle of incidence of the light-ray in each medium (1, 2, 3, etc.) at a given interface, 'n' being their refractive indices.
If the refractive index of the third medium is the same as the first and the two interfaces are parallel (e.g. light passing through air, a glass window pane and air again), the first and third light rays will be parallel; i.e. θ₁ = θ₃ (Fig 1).
If the adjacent interface surfaces are not parallel (Fig 2), even with identical 1ˢᵗ and 3ʳᵈ media a light-ray will not be parallel before and after it has passed through the 2ⁿᵈ media except under special circumstances (see 'Nodal Points' below).
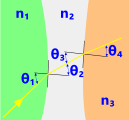
Fig 3. Concave Faces
Curving the interfaces cylindrically (2-D, Fig 3) will direct exiting light-rays according to the lens surface radii and their shapes (concave or convex), causing the exiting light-rays to converge or diverge.
Spherically curved surfaces (3-D, Fig 4) constitute a lens.
The Lens
The axis of a lens is the common centreline of both spherical faces.
A lens converges or diverges the direction of exiting light-rays by uniformly varying its thickness and opposing surface slopes (Fig 4), which it does with spherical faces, either or both of which may be convex or concave.
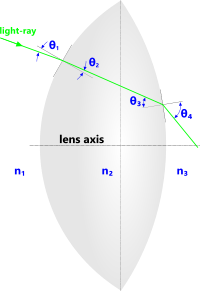
Fig 4. Convex Lens
If both spherical surfaces of a lens are on the same central axis, all of the light passing through the lens should either converge towards its axis in the case of a convex lens (as illustrated; Fig 4) or diverge away from its axis in the case of a concave lens.
The upshot of which will be to magnify (enlarge) the image at the other side of a concave lens or reduce it in the case of a convex lens. If the distance between the secondary principal point (see below) of the lens and/or the observer and/or the object being observed is sufficiently large, the image will appear inverted; i.e. the magnification will be negative.
Light-rays enter the front of a lens (the primary face)
Light-rays exit the back of a lens (the secondary face)
Nodal Points (Fig 5)
There are two nodal points on the axis of a lens, one of which coincides with the projection of an entering ray of light and the other coincides with the same ray of light projected back into the lens after it exits.
If the refractive index of the environment on both sides of the lens is the same, both nodal points will coincide with its principal points (see Principal Points below). It is important to note, however, that for any given lens this coincidence only occurs with paraxial light-rays and the principal points on its axis.
The primary nodal point is nearest to the front of the lens
The secondary nodal point is nearest to the back of the lens
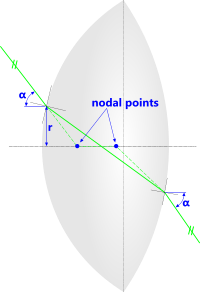
Fig 5. Nodal Points
Principal Points (Fig 6)
The principal points of a lens are where the forward projection of a ray of light entering parallel to its axis coincides with the same ray of light projected back into the lens after it exits.
Each set of principal points (secondary and primary) can be found by projecting parallel light-rays into each face (front and back) of the lens.
The primary principal point is nearest the front of the lens
The secondary principal point is nearest the back of the lens
Principal Planes (Fig 6)
The principal planes of a lens are the theoretical curved planes described by joining up its principal points.
The primary principal plane is nearest the front of the lens
The secondary principal plane is nearest the back of the lens
Focal Point (Fig 7)
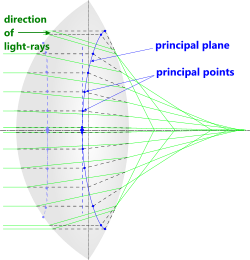
Fig 6. Principal Points
It is generally claimed that all parallel light-rays entering a convex lens will exit converging at a single point on its axis irrespective of their radial distance from the axis. This is not true. Diagrams such as that described in the left half of Fig 7 are therefore misleading.
There is always an aberration of light-rays (δf) exiting spherical lens faces that blur the image. In practice, this is overcome by using only the smallest practical diameter of the lens as aberration is significantly less in this region for similar radial variations (δr). Therefore, the clarity of an image generated through a lens is always crystal clear at the centre, becoming less so towards the periphery. I.e. the smaller the diameter of the lens used, the greater the overall clarity of the image.
The primary focal point is nearest to the front of the lens
The secondary focal point is nearest to the back of the lens
Image quality can be increased over a larger diameter by increasing the difference between the refractive indices of the lens material and the environments (both sides of the lens); i.e. a diamond lens in a vacuum will give the largest image of greatest clarity.
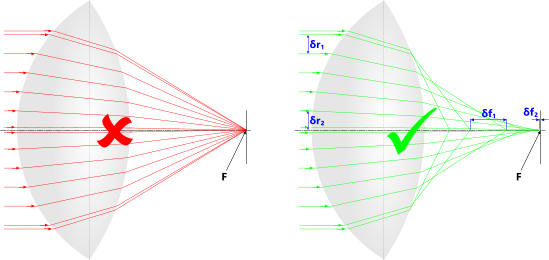
Focal Length (Fig 8)
The focal length of a lens (ƒ) is the distance between a Focal Point and its nearest Principal Point on its axis. If the refractive indices of the environments both sides of the lens are equal, both focal lengths will also be equal.
There is a well known formula used to define the secondary focal point of a lens:
1/ƒ = (n-1).[1/R₁-1/R₂+w.(n-1) / n.R₁.R₂]
The value of 1 is used in the above formula as an approximation for the refractive index of air (1.000308502), and assumes air is on both sides of the lens.
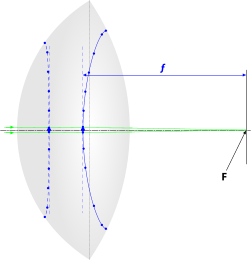
Fig 8. Focal Length
However, the above formula is an approximation. A more accurate value for the focal length of a lens can be obtained by using Snell's law to determine the focal point of a paraxial light-ray.
The differences that can be expected when using the above formula on the following lens⁽¹⁾:
R₁ = 200mm
R₂ = 300mm
w = 148mm
n = 1.631617779
are as follows:
Using 1 in the above formula: ƒ ≈ 214.575439mm
Using 1.000308502 in the above formula: ƒ ≈ 214.732956mm
Using Snell's law: ƒ = 214.732941mm
Refractive Indices
The following table lists the refractive indices for various substances:
| substance | n | substance | n | substance | n |
|---|---|---|---|---|---|
| Acetic Acid | 1.3718 | Methyl alcohol | 1.3276 | Phenol | 1.5425 |
| Acetone | 1.362 | Diethyl Ether | 1.3538 | Polystyrene | 1.59 |
| Air | 1.000308502 | Ethyl Alcohol | 1.361 | Quartz | 1.55 |
| Alum | 1.46 | Glass | 1.5 | Quartz (fused) | 1.4585 |
| Amyl alcohol | 1.41 | Glycerol | 1.473 | Ruby | 1.76 |
| Aniline | 1.59 | Flint glass | 1.65 | Salt | 1.54 |
| Asphalt | 1.635 | Ice | 1.31 | Silica (fused) | 1.46 |
| Benzene | 1.5011 | Lead | 2.6 | Sugar | 1.56 |
| Bromine | 1.66 | Mercury | 1.73 | Sulphuric acid | 1.43 |
| Carbon disulphide | 1.6276 | Mica | 1.58 | Toluene | 1.4969 |
| Carbon tetra-chloride | 1.4607 | Nitro-benzene | 1.553 | Topaz | 1.63 |
| Cedar oil | 1.52 | Olive oil | 1.48 | Turpentine | 1.48 |
| Chloroform | 1.4467 | Optical glass | 1.7 | Vacuum | 1 |
| Cinnamon oil | 1.6 | Paraffin oil | 1.43 | Water (fresh) | 1.333333 |
| Crown glass | 1.52 | Perspex | 1.49 | Water (sea) | 1.343 |
| Diamond | 2.417681113 | Petrol | 1.38 | Whale Oil | 1.46 |
Lens Calculator - Technical Help
You may find it easier to detect the reliability of input data by following the changes to the active image (Fig 9) provided in the lens calculator.
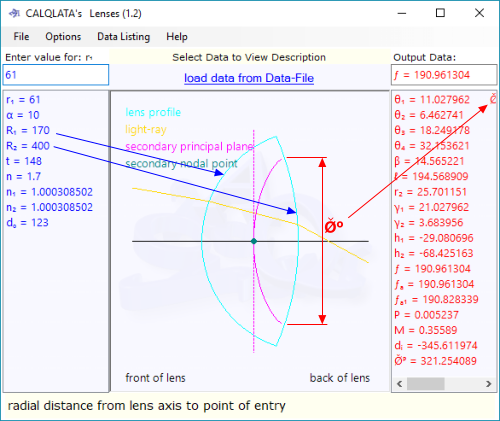
Units
You may use any units you like, but you must be consistent.
Primary and Secondary Calculations
All lenses have Primary and Secondary planes and points (see above).
The primary plane and points are generated by light entering the back of a lens. The secondary points and planes are generated from light entering the front of the lens.
Lenses only calculates the secondary plane and points generated by the light entering the Front (left-hand side) of the lens (Fig 9). If you would like to see the primary plane and points you simply turn the lens around; i.e. reverse your input values for R₁ and R₂
Input Data
r₁ = the radial distance from lens axis to the point on the surface of the front face where the light-ray enters the lens, which may be a negative or a positive value. A positive value will produce a light-ray entering the lens above its axis (in the in the active image (Fig 9)) and a negative value will produce a light-ray entering below its axis.
α = the angle of the light-ray entering the lens. If the light-ray entering the lens is to be parallel to the lens axis this value should be set to zero. A positive value will mean a clockwise rotation with respect to the lens axis and a negative value will mean an anti-clockwise rotation.
R₁ = the spherical radius of the front face of the lens (LHS). A positive value will produce a convex surface and a negative value will produce a concave surface.
R₂ = the spherical radius of the back face of the lens (RHS). A positive value will produce a convex surface and a negative value will produce a concave surface.
t = the thickness of the lens at its axis
n = the refractive index of the lens material
n₁ = the refractive index of the environment adjacent to the front of the lens
n₂ = the refractive index of the environment adjacent to the back of the lens
dₒ = the distance between the secondary principal point of the lens on its axis and the object being observed
Output Data
θ₁ = the angle an entering light-ray makes with the surface of the front face of the lens
θ₂ = the angle an internal (lens) light-ray makes with the inside surface of the front face of the lens
θ₃ = the angle an internal (lens) light-ray makes with the inside surface of the back face of the lens
θ₄ = the angle a light-ray makes with the surface of the back face of the lens after exit
β = the angle of an internal (lens) light-ray relative to the lens axis
ℓ = the horizontal distance along the axis of a lens between its secondary principal point and the intersection of a light-ray after exit. If this value is negative, the exiting light-ray will be divergent and this value defines the distance at which the projection (backwards) of the light-ray will converge with the lens axis
r₂ = the radial distance from lens axis to the point on the surface of the back face where the light-ray exits the lens, which may be a negative or a positive value indicating whether or not the light-ray has crossed the axis inside the lens
γ₁ = the angle between the lens axis and the radial distance at the point the light-ray enters its front face
γ₂ = the angle between the lens axis and the radial distance at the point the light-ray exits its back face
h₁ = the horizontal distance between the front face of the lens and the primary principal plane at its axis (negative values mean towards the right of the front face of the lens – opposite direction of the exiting light-ray)
h₂ = the horizontal distance between the back face of the lens and the secondary principal plane at its axis (negative values mean towards the left of the back face of the lens – opposite direction of the entering light-ray)
ƒ = the actual focal length of lens according to Snell's law
ƒₐ = the focal length of lens according to the standard formula (see 'Focal Length' above)
ƒₐ₁ = the approximate focal length of lens according to the standard formula assuming n₁=1 (see 'Focal Length' above)
P = the lens power (1/ƒ)
M = the lens magnification (negative value means image will be inverted)
dᵢ = the distance from secondary principal point to the [apparent] image
Ø̌ᴾ = the maximum physical lens diameter. This represents the upper limit imposed by the smaller of the two spherical radii or the point at which the spherical radii meet.
Ø̌ᴼ = the maximum optical lens diameter (Ø̌ᴾ ≤ Ø̌ᴼ) (Fig 9). If this calculated value is greater than 'Ø̌ᴾ', it will be set to 'Ø̌ᴾ'
Plot Co-ordinates (Symbols)
Secondary Principal Points:
x = horizontal distance from 'h₂' to the secondary principal point; +ve values are to the right of the principal point on the lens axis
r = radial distance from the lens axis to the secondary principal point
Nodal Points:
x = horizontal distance from 'h₂' to the nodal point; +ve values are to the right of the principal point on the lens axis (exit side of the lens)
r = radial distance from the lens axis to the light-ray at entry to the lens
α = angle about the lens axis of the light-ray at entry to the lens [degrees]
Copy and paste the above plot co-ordinates into your preferred spreadsheet in order to see their graphical interpretation.
Applicability
This calculator applies to individual optical lenses with opposing spherical faces on a common centreline (axis).
Accuracy
The lens calculator is as accurate as the data entered. There is no expected margin of error.
Notes
- Angle of incidence means the angle of the light-ray with respect to an alignment normal to the surface of the lens at the radial distance the light-ray enters the lens
- For the above mentioned lens, if the radius of the front face were altered from +200mm to -229.2mm, the focal length of all light-rays radiating from the axis to a radius of 133.57mm will be within 98% of each other, allowing one to use a much larger area of the lens’ spherical faces
Further Reading
You will find further reading on this subject in reference publications(3 & 58)

