Belt Drive Calculator
Belt drives are a means of transferring power between rotating shafts (Fig 1). Gears are normally used where the input (driver) and output (driven) shafts are close together, need accurate relative rotary positioning and/or transmit considerable power. The principal problems with geared systems are: equipment protection from excess power and the need for close positional and dimensional relationship between input and output shafts. Where equipment protection is required in a geared system, a slipping clutch may be installed in either shaft as appropriate. Geared systems are generally noisier and more expensive than belted systems.
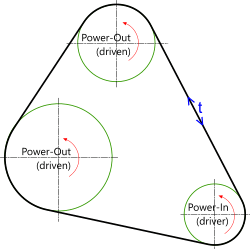
Fig 1. Typical Belt-Drive System
Belts may be toothed or plain vee-sections, or flat. Vee-belts are normally used where greater strength and frictional resistance (less slippage) is required. Teeth can be provided in either belt section where direct rotational transfer is important. Toothed belts cannot, however, provide the protection available in non-toothed belts where tension may be set to allow slippage in the event of excess input power. Flat belts are generally used for significant shaft separation distances and where slippage is unimportant.
It is important to select the right belt for the right job. Some important considerations are provided below.
Vee-Belts
Vee-belts are usually selected for applications for high-load transfer systems. It is generally considered best practice to select the lowest (appropriate) tensile belt capacity for your application minimising the rotating mass. This approach will keep the system lighter and cheaper than would otherwise be achieved by over-engineering. Belt tension should be set to provide the maximum design belt tensile capacity. The smaller the belt the greater the system flexibility, which is the primary benefit of a suitable belted system.
Toothed vee-belts should be selected on the same criteria but are used where relative rotary motion is important, i.e. slippage cannot be accommodated. If equipment protection is required for a toothed belt system, a slipping clutch will need to be installed, as would be necessary in a geared system.
Flat Belts
Flat belts are normally used for low power transfer systems with significant spacing between shafts and where slippage is inconsequential, or even expected. The pulley may be profiled with a crown to keep the belt in place.
Multiple Belts
Multiple belts may be treated as a single belt with greater power transfer capacity. However, when used for solid pulleys with multiple grooves (vee-belts) or wide profiles, it is extremely important that all the belts on the pulley are exactly the same specification and condition. Otherwise, only one belt will take almost all the load.
Contact Length
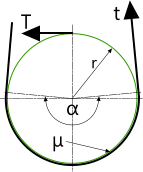
Fig 2. Friction Coefficient
The friction coefficient (μ) of any belt is directly dependent upon the length of contact it has with its pulley. A simple rule of thumb may be used to assess the grip on any pulley, based upon a design grip (μ) being achieved for a contact angle (α) of 180° (Fig 2).
E.g;
Toothed belt or chain μ = 1.0
Vee-belts μ ≈ 0.9
Flat reinforced rubber belts μ ≈ 0.8
Flat reinforced plastic belts μ ≈ 0.6
Flat leather belts μ ≈ 0.7
The torque (T) in any shaft may be estimated thus: T ≈ T.μ.α/π
It can be seen from the above formula, that widely differing pulley diameters located close together will result in the smaller pulley having a great deal less transfer capacity than the larger pulley.
This friction coefficient is not considered in the belt drive calculator because of the infinite possible variations in manufacturer specifications. Therefore, initially, you will need to estimate a belt tension for your system using Belt Drives in order to find the contact angles (α). From which you must determine the required belt tension, based upon the necessary output torque:
t = T.μ.α / π.r
and subsequently make a final calculation by applying the corrected belt tension (t).
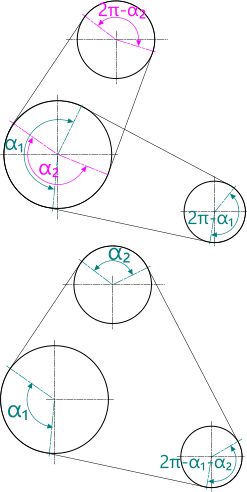
Fig 3. Multi-Stage Belt Systems
Power is the same in the input and output shaft as long as slippage does not occur.
Torque and rotational speed will vary according to pulley diameters.
Multi vs Single Stage
The total contact angle in a belt system always adds up to 360°. Therefore, the contact angle (per pulley) in a properly designed 2-pulley system will always provide greater contact length than an equivalent 3-pulley system. Therefore, it may in some circumstances be preferable to use two belts and four pulleys to transfer load to two output shafts where each pair achieves greater contact length (per pulley) than the 3-pulley system would achieve (Fig 3). Such an approach would allow the use of smaller belts.
Belt Drive Calculator - Technical Help
Units
You may use any units you like, but you must be consistent.
Except where square brackets [] designate the units you must use.
Input Data
t: The maxim tension you expect to be taken in the belt
rᵢ: The radius of the contact surface between the belt and the pulley
Nₒ: The rotational speed of the output pulley in revolutions per second
x,y: The co-ordinates of two pulley centres
R: The distance between two pulley centres
Output Data:
P: The power generated in the system
N: The rotational speed of pulleys in revolutions per second
T: The torque induced by the belt in a given pulley
v: The curvilinear speed of the belt
αᵢ: The angle of contact between the belt and the pulley in degrees
ℓ: The length of belt in contact with the pulley
L: The total length of belt required to circumnavigate the pulleys
F: The force required to apply the tension in the belt
θ: The angle between the pulley centres in a three-pulley system
Applicability
Belt Drives may be used for any pulley system around which a flexible cord, such as ropes, belts, chains, etc., is used to transmit power between driver and driven shafts.
Accuracy
Belt Drives' output data will be as accurate as the input data.
Further Reading
You will find further reading on this subject in reference publications(1, 2 & 3)

