Electrical Current Calculator [Volts, Amps, Ohms]

Fig 1. Water in Pipe vs Electricity in Cable
As electricity can be a difficult concept for those who are unfamiliar with the subject, we shall use a pipeline analogy for all the electrical properties, which we hope will help your understanding. Imagine flowing electricity as water flowing through a pipe (Fig 1) {pipeline analogies are normally enclosed in curly brackets}.
Conductor (electrical)
This is the means by which electricity may be transported from one place to another {think of this as the pipe}. We shall refer to the conductor as a 'cable' although it is known as a 'wire', 'cord' or 'conductor'. It can take any shape or form but is normally one or more (multi-strand) circular-section wire covered by an insulating material. The reason why multi-strand cables are used rather than single-core wires of the same diameter, which would provide lower resistance, is that large diameter cables used for high-current transmission would be very difficult to bend.
A good conductor allows the electricity {or water} to flow through it very quickly and with little effort.
A bad conductor will make it very difficult for the electricity {or water} to flow through, making it a good resistor.
Electricity (DC/AC)
Electricity is the unusually intense transfer of electrons between adjacent atoms in a conductor, all in the same direction. The quantity of electricity passing along the conductor is measured in coulombs {imagine this as the gallons or litres of water passing along the pipe}.
'DC' electricity means direct current. It is continuous and should be regarded as equivalent to the flow of water through a pipe generated by a vane or centrifugal pump: i.e. it provides constant flow in one direction.
Whilst DC current (and voltage) is generally provided by a battery or other power storage facility, a slightly different version can also be created by a DC generator (see CalQlata's MotAtor calculator). 'DC' is normally used for relatively low power supplies (<100 Watts) such as portable electrical and electronic equipment, e.g. mobile telephones, computers, etc. The advantage of a battery power supply is that it is a simple system that does not require a generator (until your battery needs recharging, that is).
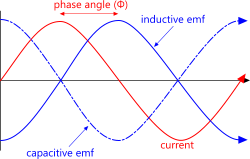
Fig 2. Alternating Current
'AC' electricity means alternating current. It varies between positive and negative {imagine water being forced along a pipe using a piston pump (i.e. push-suck-push, etc.)}. AC current (and voltage) is provided by rotating a strong magnet in a series of wire loops.
Whilst the voltage also alternates at the same frequency as the current, it does not normally do so at the same time, i.e. they will normally be 'out-of-phase' (Fig 2). The number of times this alternation occurs each second is called the frequency ('ƒ') of the electricity and is measured in hertz (Hz).
The electrical current calculator is limited to single phase AC power supply calculations (as shown in Fig 2). A three-phase electrical power supply induces three single-phase supplies each of which is out-of-phase by 120°.
The transport of electrical power in a cable is limited by its electrical resistance, which is pre-defined by its; material⁽²⁾, length, diameter and temperature. Joule's first law states; 'power loss in a conductor is proportional to the square of the current (p = I².R)', but as it is also proportional to the Volts (p = V.I) you should try to keep the current as low as possible and the voltage accordingly higher when designing electrical power transmission systems. You do this with transformers.
Voltage [Volts]
Voltage is the force that creates the flow of electricity {imagine voltage as the pressure drop across a pipe}. It is also known as the electro-motive force (emf) and the potential difference (pd).
Current [Amps]
The current is the rate (or speed) at which a quantity of electricity flows through a conductor {i.e. the gallons or litres per minute}. One Amp is the passage of one coulomb of electricity per second.
Impedance [Ohms]
Impedance is the total resistance in a conductor. It includes the static Resistance ever-present as a result of its material resistivity, its dimensions and its temperature, along with the Reactance generated in AC electrical supply.
As Impedance² = Reactance² + Resistance², impedance will always equal resistance in DC electrical circuits as reactance is zero. But in AC electrical supplies, resistance will always be present to some extent and is responsible for shifting the phase angle (Fig 2) between voltage and current.
Resistance [Ohms]
Returning to our 'pipe' analogy, think of a resistance-free circuit as a fully open, absolutely straight, clean, friction free pipe of slightly increasing diameter with water being pumped into the small end and pouring out of the other. This is an excellent means of transporting water (or electricity) from one place to another with minimal losses and without its doing any work.
If, however, you install a helical (or screw-type) vane in our pipe that is in some way connected to a free-running wheel outside the pipe, the wheel will rotate as the vane rotates thereby doing work, but this work will require; a) sufficient pressure (voltage) to generate the flow rate, and, b) sufficient flow rate (current) to rotate the vane. The resistance experienced in the system in order to rotate the helical vane is equivalent to the electrical resistance in a conductor.
High resistance in a conductor can be useful;
e.g. for an electric light-bulb filament where it will heat up sufficiently to make it glow
or a bad thing;
e.g. in a long-distance carrier of electricity where high resistance will require high power to transmit and the consequent heating of the conductor will result in losses at the supply end
Reactance (AC current) [Ohms]
Reactance is AC electrical resistance generated by Inductance or Capacitance both of which are independent of Resistance.
Inductance (AC current) [henrys]
The 'applied' emf created by an AC generator provides the force that drives the growth of the alternating current during its cycle (Fig 2). Inductance is the resistance generated by the induced (or 'back') emf which opposes the applied emf and therefore retards the growth of the current. It is this retardation of current flow by the 'back' emf that creates inductive resistance.
The current peaks after inductive emf and is therefore said to lag the voltage (Fig 2).
Capacitance (AC current) [farads]
Capacitance can be thought of as an electrical diaphragm building up energy {pressure} as the voltage increases and preventing current flow, but unlike a physical diaphragm it doesn't stop all flow. A capacitor collects electricity as AC current grows through its cycle and releases it as the current falls. It is this flow prevention during the cycle that creates capacitive resistance.
The current peaks before conductive emf and is therefore said to lead the voltage (Fig 2).
Power [Watts or Joules per second]
The power ('p') in the circuit is a means whereby we can define the rate of work done by the electricity {or water} whilst passing through the conductor. For DC power supplies this is simply Volts x Amps, but AC power supplies are attributed 'True' and 'Apparent' power ratings.
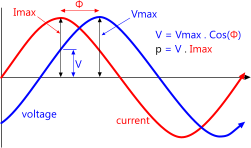
Fig 3. True Power Calculation
Power Factor (AC current)
The power factor is the factor by which the apparent power is reduced to account for the phase shift from combining Resistance and Reactance. It is also equal to the Cosine of the phase angle (Cos(φ)).
True Power (AC current)
True power is the maximum current (Imax) multiplied by the coincident voltage (V), where Volts is Vmax multiplied by power factor (Fig 3).
Apparent Power (AC current)
Apparent power is the maximum current multiplied by the maximum voltage without the application of a power factor (see above) and is usually referred to as the kVA (kiloVolt-Amp) rating of a power supply
Electrical Current Calculator - Technical Help
The difference between the AC-DC and Power Transmission calculation options is that 'AC-DC' only calculates the theoretical relationships between the various properties of an electrical charge, whereas 'Power Transmission' relates these properties to an electrical cable (or conductor).
Example Calculation (a fictitious 50W x 240V light-bulb filament Figs 4 & 5)
1) Select calculation option: AC/DC
2) Enter 50 [Hz] for frequency (e.g. domestic frequency in the UK)
3) Enter 220 [V] for voltage (e.g. mains voltage in UK homes)
4) Enter 2.8 [h] for inductance (typical for UK mains)
5) Select calculation option: Power Transmission
6) Enter 3.5E-05 [m] filament diameter (about 1.4 thou)
7) Enter 0.58 [m] filament length
8) Enter the properties for tungsten; αᴿ; 0.004403 [/°C], ρᴿ; 5.5E-08 [Ω.m], cp; 134 [J/kg/K] and ρ; 19293 [kg/m³]
9) Enter 2500 [°C] for the temperature you need to achieve
10) Enter 1 for the number of filaments (the calculation is now complete)
11) Copy the result for Resistance (398.123037)
12) Return to AC/DC and paste the resistance value into the appropriate input data ('R')
You will notice that power ('p') is 50 in calculation option 'Power Transmission' and 20.67 in calculation option 'AC/DC'. This is because power in 'Power Transmission' is apparent power ('ap'; 0.05kVA⁽⁴⁾) whilst power in calculation option 'AC/DC' is true power (20.67W⁽⁴⁾). The above filament has been designed for 50VA⁽⁴⁾ (as opposed to 50W⁽⁴⁾)
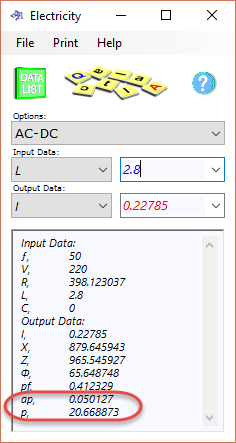
Fig 4. AC-DC
AC-DC
This calculation option is for calculating general relationships between electrical properties without considering the electrical conductor.
The voltage and current in a direct current (DC) circuit are both constant. They have no frequency. As such, if you delete the input value for frequency ('ƒ') or set it to zero, the electrical current calculator will automatically assume you're performing a DC calculation. In this case, neither Inductance ('L') nor Capacitance ('C') will be included in the calculation and all output data except current ('I') and power ('p') will be automatically set to zero.
However, if you need to calculate the electrical resistance of a conductor using this calculation option, you may use Power Transmission (see below) to calculate its Resistance ('R') from its material, dimensions and temperature, and copy and paste the result into this option (remembering to remove any commas from the data).
The value you enter for voltage ('V') or get for Reactance ('X') in this calculation option will be automatically inserted into the appropriate input data in the in Power Transmission calculation option the next time you select it.
Re. power and apparent power output values, see 'Note 4' at the bottom of this page
Power Transmission
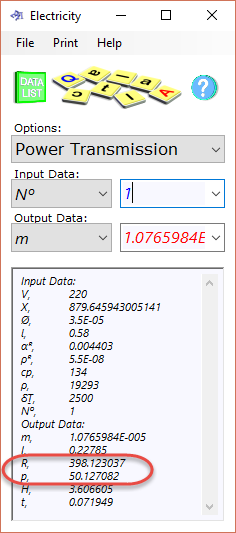
Fig 5. Power Transmission
This calculation option is for identifying the performance of an electrical transmission cable (or conductor).
The values for Voltage ('V') and Reactance ('X') in this calculation option are automatically transferred from AC/DC and the appropriate output value for Resistivity ('ρᴿ') is automatically transferred from Resistivity/Conductivity each time you enter this calculation option. However, whilst you remain in this calculation option, the electrical current calculator will incorporate any modifications you make to these input data values.
This calculation procedure has been designed to enable you to enter your conductor materials, dimensions and design temperature to achieve the desired working conditions. You can use it to calculate the properties of an incandescent metal-filament light-bulb or limit the operating temperature of a power carrying cable. For example:
A light-bulb filamentThe purpose of a light-bulb filament is to glow as brightly as possible. In the case of a metal wire filament its brightness is directly proportional to its temperature irrespective of the material from which it is made. Therefore, it is obviously better to use a metal with the highest melting temperature (e.g. tungsten) and get it as hot as you can without risking short-term failure, remembering of course that if its normal operating temperature is too hot it will fatigue with frequent switching 'on' and 'off'. the elctrical current calculator has inserted the properties of a fictitious 240V x 50W light-bulb in the menu item 'Files>Reset to Default Data' where the appropriate properties for a Tungsten filament have been extracted from CalQlata's Metals database.
A transmission cableThis is a much easier proposition as you only need to identify the maximum permissible temperature and you will of course know what power you have available.
For example, if you want to see how much power you can transmit from your power-station over 300 km through a 15mm aluminium alloy diameter cable, the temperature of which cannot rise by more than 50°C ...
... you enter the physical properties of your cable along with the properties of the power you want to transport (1.0E+07W) say 220,000V and 45A (use 24h for inductance in this example⁽³⁾) and you get 6.6 megaWatts.
Your only problem is to make sure that the heat produced 7E+09J can be lost from its surface area in less than 1089 seconds (see CalQlata's Thermal Conductivity calculator), which is the time it takes for the power to generate sufficient heat to achieve the maximum permissible temperature.
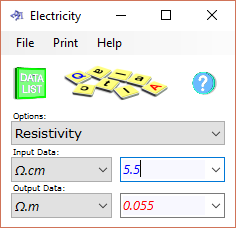
Fig 6a. Resistivity
Resistivity (conductivity)
Resistivity (Ω.m) is equal to the reciprocal of conductivity (S/m)
The natural resistivity that exists in every material defines the level of resistance it has to an electrical current passing through it⁽²⁾. The industry uses many different versions of the units but the most common are: a) metric; μΩ.cm and b) imperial; Ω.c-mil/ft
Whilst the electrical current calculator uses only Ω.m for resistivity in all its calculations this calculation option includes a facility to convert between 54 resistivity and conductivity unit alternatives. But because the conversion potential is so large the sub-divisions and multiples of Ohms and Siemens are not included as this would make the selection list impractically large. (Fig 6a)
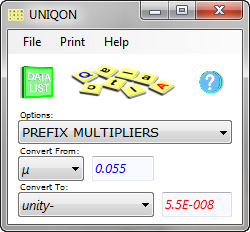
Fig 6b. Unit of Resistance Conversion
If you want to convert μΩ.cm into Ω.cm simply multiply the value you have by the appropriate multiple 'μ' (5.5E-06).
If you want to convert Ω.cm into μΩ.cm simply divide the value you have by the appropriate multiple 'μ' (5.5E+06).
Or you could use CalQlata's UniQon calculator, which would do this for you (Fig 6b).
This calculation option also includes the IACS% calculation as set by 'The International Annealed Copper Standard' for a copper comparison.
Notes
- The difference between a DC generator and an AC generator is simply the method used for extracting the current.
- The resistivity of some materials does not rise with temperature some actually fall (e.g. some carbon composite materials)
- Self-Inductance from a generator is normally defined thus: Voltage = Inductance x change in current ÷ change in time. In the example shown above (A Transmission Cable) a frequency of 50Hz is assumed making the change in time 0.01 seconds for the current to change from minimum to maximum (-45A to +45A). This property is not calculated in the electrical current calculator as it varies considerably dependent upon self-induction, induced emf, type of alternating current, etc.
- If the difference between power and apparent power appears at first sight to be adrift by a factor of about 1000 it is because power is specified in Watts and apparent power in kVA (kiloVolt-Amps) according to convention.
Further Reading
You will find further reading on this subject in reference publications(3, 11, 21 & 22)

