Pipe Flow Calculator (liquid or gas)

The behaviour of single-phase fluid flow in a pipe will depend upon the properties of the fluid and the pipe and what you do to the fluid in order to force it through the pipe. This behaviour will also vary across the diameter of the pipe (i.e. at 'r').

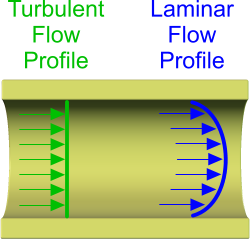
Fig 1. Flow Profiles

Laminar Flow

Under Laminar pipe flow conditions the layer⁽¹⁾ of fluid adjacent to the internal wall of the pipe will be slowest due to interaction with the surface of the pipe wall (see Fig 1). This interaction is due to a combination of the drag from the uneven surface of the pipe wall and the surface tension in the fluid. Fluid further away from the wall will travel progressively faster until the combined flow rate is a) sufficient to account for the volumetric flow rate and b) the pipe wall's influence on the fluid becomes insignificant.

Turbulent Flow

Under Turbulent pipe flow, fluid particles will not be travelling in a straight line. Each layer⁽¹⁾ in the flowing fluid will therefore influence each adjacent layer slowing it down. The overall effect of this behaviour will be to approximately equalise the velocity of the fluid across the diameter of the pipe (see Fig 1).

Liquids

Every liquid is incompressible. That is, its density cannot change as a result of physical deformation⁽²⁾. Therefore, whatever you push in one end of a pipe will come out of the other end in almost the same condition. The term 'almost' must be applied here because the work done in pushing the liquid through the pipe will produce losses through friction that will increase the temperature of the liquid affecting its density. This effect is not addressed in PipeFlow.

The pressure-drop (δp) is calculated to define the pressure necessary to push the liquid through the pipe. It is this value (along with the flow rate) that must be exceeded by your pump if the liquid is to pass through the pipe using your equipment.

Pipe flow velocity of the liquid at the pipe wall is important because; if there are any gas bubbles or solid particles in the liquid, pipe material erosion is likely to occur if the velocity is excessive. The level of erosion is dependent upon the quantity of particles and the material from which the pipe has been manufactured. Whilst the actual level of erosion can only be ascertained by physical testing, some specifications and standards provide recommended pipe flow-rate limits to prevent this phenomenon (see CalQlata's APIpe calculator).

Gases

Every gas is compressible. That is, its properties will change due to pressure and temperature. Therefore, whatever you push in one end of a pipe will not come out of the other end in the same condition. These effects are accounted for in PipeFlow.

You define the pressure drop (input pressure minus ambient or output pressure) along the pipe and the pipe flow calculator will do the rest.

Gas velocity is also important because if there are any entrained solid or liquid (condensation) particles present, pipe material erosion is likely to occur if the velocity is excessive (see CalQlata's APIpe calculator).

Pipe Flow Calculator - Technical Help

Units

You may use any units you like, but you must be consistent.

The Pipe

Whilst typical values for surface roughness (ϵ), i.e. the depth of surface irregularities, are provided in the technical help facility of the pipe flow calculator (for steel, concrete, plastic, etc.), you can of course enter any measured or third-party value you like.

The effect of bends and constrictions are not considered in the pipe flow calculator. If pipe-bends are designed and manufactured correctly they will have little effect on fluid performance. However, badly made pipe-bends and joints will accelerate localised erosion (see 'Liquid Flow' & 'Gase Flow' above).

Liquid Flow

For liquid flow in the pipe flow calculator, you enter the pipe details and the quantity flow rate (e.g. m³/s) you require, along with the properties of the liquid, and the pipe flow calculator will tell you what will happen to it in the pipe.

The properties of most liquids can be found in CalQlata's Liquids database.

Fig 2. Fluid Head-In vs Head-Out

The difference between the heads at the inlet and outlet ends of the pipe is akin to the pressure drop between inlet and outlet ends. You enter the height between the surface of the feed liquid and the 'inlet' location for the pipe (Z₁), and the height of the other end (H; Fig 2) of the pipe and PipeFlow will calculate the resultant head at the outlet end (Z₂). A configuration such as that shown in Fig 2 will result in a negative head at the outlet end of the pipe.

For the purpose of these calculations, the tortuous route taken by the pipe to get to the other end is irrelevant. Only the change in height matters here.

Gaseous Flow

For gas flow in the pipe flow calculator, you enter the pressure drop you expect, along with the pipe details and the gas properties, and PipeFlow will calculate the condition of the gas at entry and exit.

The properties of most gases can be found in CalQlata's Gases database.

The difference between the inlet and outlet head is ignored for gas flow calculations due to the minimal difference between the density of air and that of most other gases that will generate a negligible head irrespective of practical height variations.

If you have 1bar (100000N/m²) pressure {atmospheric pressure} at the outlet end of the pipe, which is the norm, all you have to know is the pressure you will apply at the inlet end. PipeFlow will do the rest.

Notes

The term layer is descriptive only. Fluids do not separate into discrete layers when flowing through a pipe.
This is not strictly true of course. All matter is compressible, even seawater, which is denser at the ocean floor than it is at the surface. Incompressible in this sense actually means virtually incompressible.