Areas and Volumes Calculator
Volumes calculates the dimensions, displaced space of common, regular, solid shapes and areas defines their surface and profile areas in part and/or in full.
You can use CalQlata's 2ND Moment of Area and 2ND Moment of Area+ calculators to calculate the cross-sectional area of hollow and solid, regular and irregular shapes.
Profile Areas
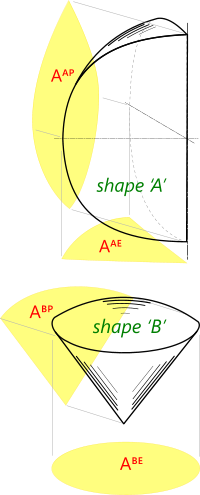
Fig 1. Spheres and Segments
Profile areas (Figs 1 and 2) are the side (Aᴾ) and end (Aᴱ) areas projected onto a flat surface, which are used in Drag and Added Mass calculations
(see CalQlata's Added Mass & Drag calculator).
Shapes
Volumes calculates the volume and key areas of the following common shapes:
Pyramidal-Prism
Conical-Prism
Barrel
Sphere
Torus
Pyramid-Prism
This option calculates the properties of a prism with a given number of sloping sides of the same size and shape.
I.e. a regular (all sides dimensionally equal);
Pyramid: set b₂ to 0
or
Frustum: set 0 > b₂ ≤ b₁
with 3 or more sides.
You can calculate the properties of any regular polygonal bar of constant cross-section; by setting n to the number of sides and b₁ and b₂ dimensionally equal.
Cone-Cylinder
This option calculates the properties of a cone,
which is a pyramid with an infinite number of sides
(an elliptical section) or a regular;
Cone: set Ø₂ to 0
or
Frustum: set 0 > Ø₂ ≤ Ø₁
The properties of a regular cylinder, with parallel sides, are calculated by setting Ø₁ equal to Ø₂
Barrel
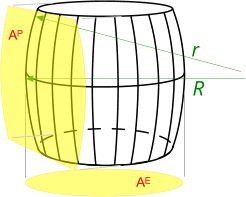
Fig 2. Barrel Areas and Volumes
There are two commonly used barrel shapes:
The 'circular' type is easier to make and generally used for small volumes (masses).
Radii 'R' and 'r' (Fig 2) are dimensionally equal for this barrel. In fact the longitudinal sectional shape of this barrel constitutes part of a large circle.
The 'parabolic' barrel is much stronger and normally used for large volumes (masses).
Radius 'R' is larger than 'r' (Fig 2) for this barrel. The parabolic nature of its section flattens this barrel out at the waist.
SPHERE
This calculation is for the areas and volumes of segments (Shape A) and sectors (Shape B) of a sphere, both of which are calculated using the same input data and the results for both are generated with every calculation. If you enter negative values or angles greater than 360° you will get answers that are theoretically correct, but you will need to be careful how you interpret them.
The profile areas of these shapes are indicated in Fig 1. If you enter an angle for θ greater than 180° the profile projected area for Shape A (Aᴬᴾ) and the base projected area for Shape B (Aᴮᴱ) will always be the same as that for a complete and full-size circle. The other two (Aᴬᴱ & Aᴮᴾ) will vary according to the shape created by the angle entered.
You need to enter an angle for θ of 360° for a complete sphere.
Torus
This area and volume calculation option is considered self-evident and therefore not addressed further here.
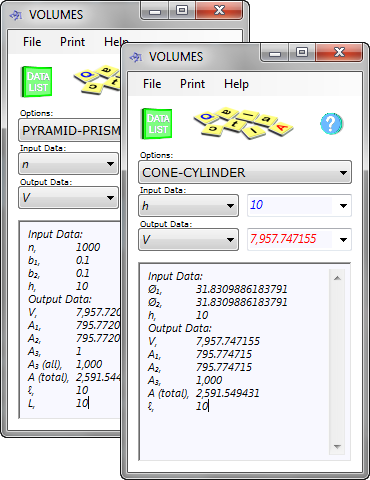
Fig 3. Self-Checking Calculation
Areas and Volumes Calculator - Technical Help
Units
You may use any units you like, but you must be consistent.
Self-Check
'PYRAMID-PRISM' and 'CONE-CYLINDER' calculation options provide a self-checking facility in that you can set b₁ and b₂ to 0.1 and the number of sides (n) to 1000 in calculation option 'PYRAMID-PRISM' and compare the results to a cylinder with a diameter (Ø₁ & Ø₂) of 31.8309886183791 in calculation option 'CONE-CYLINDER'.
You should get the same results in both (see Fig 3).
Accuracy
There is no margin of
error in these calculations.
Your answers will be as
accurate as your input data.
Further Reading
You will find further reading on this subject in reference publications(3 & 12)

