Fluid Forces Calculator (Morison's Equations)
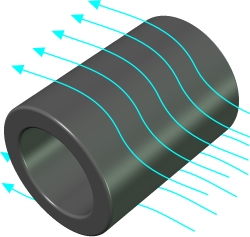
Fig 1. Fluid Flow Over a Tubular Body
When fluid flows over a stationary or moving body, there are two distinct forces trying to slow it down:
1) The force created by the interface resistance between a fluid and the surface of a body. This effect is called 'Drag', which is defined by a 'Drag coefficient' (< 1.0) and is dependent on the relative velocity between the fluid and the body. The combination of body surface finish (roughness and/or tackiness) and fluid surface tension (its resistance to shear) will together with the shape of the body define this fluid force.
2) The force required to displace a volume of fluid by a body moving through it. In this case, the displaced fluid is assumed to occupy a volume at least equal to the body displacing it and is called an 'Inertia coefficient' (> 1.0). This force is dependent on the relative acceleration between the fluid and the body.
Drag, Added Mass & Inertia Coefficients
A force imposed on a body by a flowing fluid is due to, and depends upon, the above interactions.
The fluid force due to drag comes from the slowing down of the fluid directly in contact with the body as a result of skin friction and the fluid's surface tension. Drag increases in proportion to the body's surface roughness. There would be no drag at all on a body if it was totally frictionless (impossible), i.e. the coefficient of friction would be zero irrespective of its shape. Once one accepts that there is no such thing as a frictionless surface, the shape of the object (facing the fluid flow) and its position relative to an adjacent boundary will directly affect its drag coefficient.
For example;
a) The Drag coefficient for a pointed body with a small included angle and a highly polished surface will be somewhere between 0.2 and 0.5
b) The Drag coefficient for a round body mid-stream and a normal surface will be somewhere between 0.5 and 0.7
c) The Drag coefficient for a round body positioned less than one diameter away from a solid boundary and a rough surface will be somewhere between 0.7 and 0.9
d) The Drag coefficient for a flat body mid-stream and a rough surface will be somewhere between 0.9 and 1.0
e) For wave 'slam' (a boundary condition where the body passes from air to water), it is normal practice to increase this value to between 2.0 and 5.0 to allow for dynamic effects. 2.0 should be used for a glancing blow and 5.0 for maximum impact conditions.
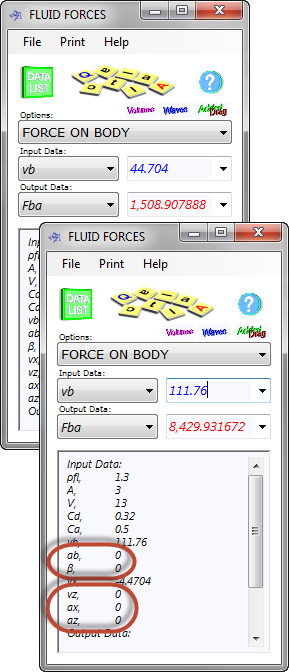
Fig 2. Simple Fluid Force Calculation
2) A force resulting from mass displacement is defined by the Inertia Coefficient, which is the sum of the coefficients for the fluid actually displaced by the body (=1.0) and the Added Mass coefficient (≤1.0). The added mass represents the volume of fluid disturbed by an immersed body exposed to relative movement over and above the volume displaced by the body itself. This coefficient is normally between 0.25 and 0.75
a) The Added Mass coefficient for a pointed body with a small included angle and a highly polished surface will be somewhere between 0.3 and 0.4
b) The Added Mass coefficient for a round body mid-stream and a normal surface will be somewhere between 0.4 and 0.6
c) The Added Mass coefficient for a round body positioned less than one diameter away from a solid boundary and a rough surface will be somewhere between 0.5 and 0.8
d) The Added Mass coefficient for a flat body mid-stream and a rough surface will be somewhere between 0.7 and 0.9
3) Where a body is moving relative to a fluid, you need to include the total displaced mass (added mass plus actual mass of displaced water) multiplied by the acceleration of the body in your force calculations.
4) An added mass coefficient of 1.0 is normally added the actual displaced mass for unknown conditions. In such cases, the virtual (or inertia) mass coefficient is normally taken as 2.0.
You enter only the 'Added Mass' coefficient in the fluid forces calculator, which will automatically convert this value into an 'Inertia Coefficient' by adding 1.0 to it in the calculations.
The above values are provided for guidance only. Accurate values should be calculated using tried and tested methods or CalQlata's Added Drag program (see Data Import Facility below).
Fluid Force Calculator
Technical Help
CalQlata's Fluid Forces calculator addresses forces on:
a) a body passing through a fluid,
b) a fluid passing over a body, and
c) a combination of 'a' and 'b' according to the equations established by Morison
Units
You may use any units you like, but you must be consistent.
You should apply suitable additional factors to Cd and Ca that take account of significant surface roughness and/or relative proximity of the body to a surface preventing free-flowing orbital fluid, either of which can significantly increase their values (see CalQlata's Added Drag calculator).
Important: You should remember that the 'Force' results will be in the form of 'mass multiplied by acceleration' {e.g. Newtons}. As such your input mass values {e.g. kilograms} must not include the effects of gravity.
Terminal Velocity
In a vacuum, a falling body would continue to accelerate, increasing its velocity indefinitely or until impact. This is not the case for a body falling through a fluid (a gas or a liquid) under the influence of gravity. When the force of the falling body due to its mass and gravitational acceleration is equal to the fluid force slowing it down, the body will stop accelerating and continue to fall at a constant velocity, i.e. its 'terminal velocity', until impact.
Any fluid, even a gas (e.g. air) will stop a body accelerating, and water will do this very quickly indeed. For example: drop a house brick 'end-on' in air and it will take 8 seconds and 200m to reach its terminal velocity of about 80 m/s. Drop it in water, 'end-on' and it will take only 30mm and 1/10th of a second to reach its terminal velocity of about 1 m/s.
Force on a Body
In this calculation, you input the body and fluid information at an instant in time, and the Fluid Forces calculator will provide you with:
a) The vertical and horizontal force on the body induced by the moving fluid
b) The vector force on the body due to resolving a) above
c) The force on the nose of the body (axial force) as it passes through the fluid in the vector direction at the velocity you have entered for the body
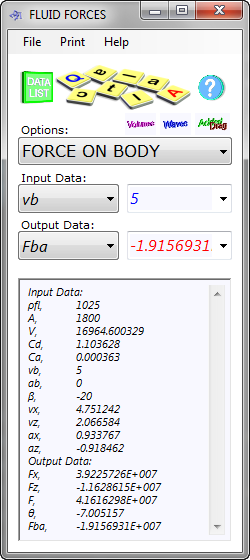
Fig 3. Complex Fluid Force Calculation
This calculation requires a lot of input if you are looking for a complex result, but if you simply want to find out for, example, the force on the front of a car driving at 100 mph (44.704 m/s) through a 10mph (4.4704 m/s) head-wind, where the frontal resistance from the air is about 1,509N (154kgf), you can ignore a lot of the input (see Fig 2). Increase this to Bugatti Veyron speeds and the force required to push the air out of the way is getting on for a tonne: 8430N (860 kgf; see Fig 2).
For more complex calculations, e.g.; the resistance a submarine will experience travelling 20° down through seawater at 10 knots (5 m/s), 20m below sea level and in 20m waves (resulting in an axial force of nearly 2000 tonnes; see Fig 3): either you can calculate the wave, current and shape coefficient values yourself or you can import the data (see Data Import Facility below) leaving the only manual inputs as body velocity ('vb') and direction ('β'), in this case as acceleration ('ab') is zero.
Note: The submarine is a very theoretical case for wave loading, as water particle velocities will vary continually along the length of a 150m long object passing through one in any direction other than parallel. Except under very special circumstances, it is normal to evaluate the effect of current only on such large objects in the ocean.
Data Import
Fluid Forces provides a data import facility for you to extract information from three other 'export' calculators (Waves (ocean), Volumes and Added Drag) if they have been installed.
The information retrieved from Added Drag is the drag coefficient (Cd) and the added mass coefficient (Ca).
The information retrieved from Volumes is the body volume and profile area (V & A).
The information retrieved from Waves (ocean) is the vertical and horizontal water particle velocities (vx & vz) and accelerations (ax & az).
Fluid Forces automatically inserts the side profile area from Volumes and assumes that if you are using data from the calculation of ocean waves, the fluid density must be that of seawater. If you need to change either of these values, then you should do so after importing from the associated Data File.
Important: You should not forget to save the calculation data in the export calculators before trying to load it into Fluid Forces.
Further Reading
You will find further reading on this subject in reference publications(6, 8 & 9)

