Beam Strength and Deflection Calculator
A beam or bar is any structural member significantly longer than it is wide or deep. The term 'significantly', however, means different things to different people. To some people, twice as long is sufficient, others would consider five times as long to be too short and would therefore consider such a member to be a plate, a frame or a structure. Beams' calculation procedures impose no such limits or distinctions.
Beams are normally used to carry a load whilst spanning supports a good distance apart, such as a floor (see CalQlata's Floors calculator). When specifying a beam you must define its maximum loading capacity (i.e. its strength) and its maximum acceptable deflection.
Beam Strength and Rigidity
The strength of a beam is dependent upon the yield stress of the material from which the beam is manufactured, thereby defining the maximum load that may be applied before it will permanently deform (or break if made from a brittle material), and
its rigidity is dependent upon the second moment of area of the beam's cross section (e.g. Channel, I-Beam, H-Beam, Angle, etc.) along with the Young's modulus of its material, thereby defining the expected deflection in the beam for any given load
Both the above characteristics define the behaviour of a beam under load.
Design a Beam
Assume you have an evenly distributed load of 4000N over a beam length of 4m (1N/mm) and a maximum permissible deflection of say 1/200th of the beam's length (20mm).
Using Beams you enter the information you know and modify the second moment of area (I) until you get the desired deflection (20mm in the middle of the beam where its deflection will be the greatest), which in this case, gives you a value for I of about 800000mm⁴.
Assuming you plan to use a Channel section, by sorting the Channels in CalQlata's Steel Sections database you find that your beam size should be a '3x6' section which is the smallest beam section with an I value above 800000mm⁴ and find the value for 'y' (the distance from the beam's neutral axis to the outside of its section), which in this case is 38.1mm.
You return to Beams, enter the correct value for I (863,264mm⁴) and also enter the value of 38.1mm for 'd' to establish the maximum stress in the beam material, which in this case is 88N/mm².
If this value is within your safety margin requirements then your beam is acceptable. If not, but you have to work with a given material, then you should change (increase) the beam section thereby reducing acceptable deflection until the stress is acceptable.
Beam Deflection Calculator - Technical Help
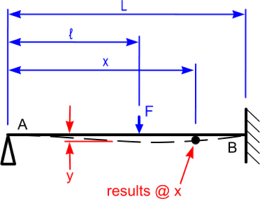
Fig 1. Beam Loading Diagram
Any load in the Beams strength calculator is assumed to apply equally through the plane or section of the beam in all directions normal to (in other words, @ 90° to) its longitudinal axis.
If the load is localised within the beam's cross section (i.e. not evenly distributed through it), additional calculations may be required to identify local (concentrated) reactions and stresses (see CalQlata's Plates and SHEETS calculators).
Bending Stress
Bending stresses in Beams apply to the beam a specified distance ('d') out from its neutral axis. This input variable ('d') is used only in the calculations for stress (σx) and strain (ex). If you leave it blank or set it to zero, Beams will not calculate stress or strain at your designated position along the beam (Fig 1 'x'). None of the other results will be affected.
Multiple / Simultaneous Loading Conditions
Should you have a beam with more than one applied load you simply add the results together at your specified location.
Beam Strength Calculation Example (Fig 2):
Beam details:
L = 2000 mm
I = 1.2E+08 mm⁴
E = 2.07E+05 N/mm²
y = 200 mm
Loading condition 1:
wA & wB = 450 N/mm
l = 0
Loading condition 2:
F = 150000 N
l = 700 mm
Distance along beam to Output:
x = 1000
Step 1:
Enter data for the beam and Loading Condition 1 (Simple-Fixed / Distributed Load) setting wA (/L) and wB (/L) to 450' copy Data Listing and paste into a spreadsheet.
Step 2:
Enter Loading Condition 2 (Simple-Fixed / Point Load) setting F to 150000, copy Data Listing and paste into the same spreadsheet.
Step 3:
Add results from both calculators and you will have the conditions at the location required.
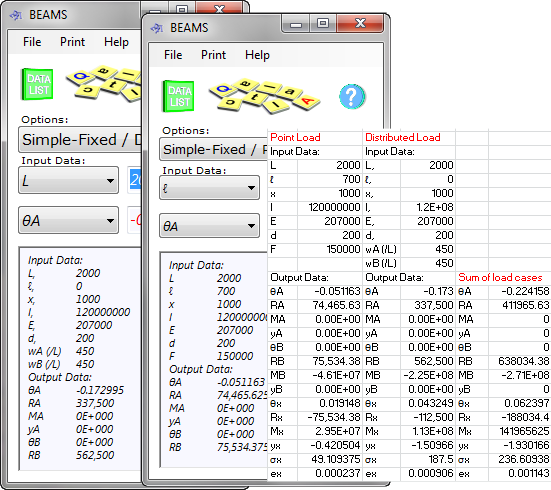
Fig 2. Compound Loading Calculation Procedure
Limitations
These calculations are only valid whilst the material throughout its length and sectional thickness obeys Hooke's law.
The results remain valid for this calculator if the deflection is such that the length of the beam is not significantly affected by the loading conditions.
CalQlata's large deflection beams calculator (Flexible Beams) should be used where beam length changes by more than 5% as a result of the applied load.
Units
You may use any units you like, but you must be consistent.
Further Reading
You will find further reading on this subject in reference publications(2, 3 & 4)

